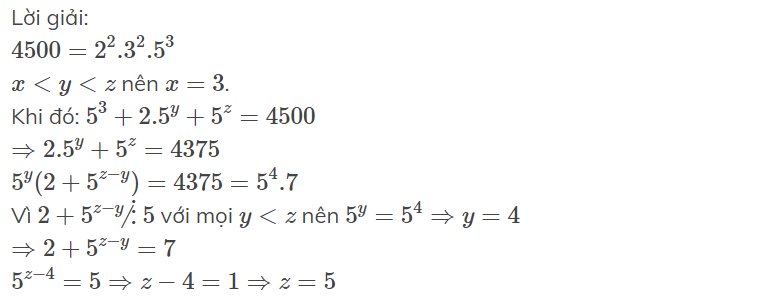K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LT
0

Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
1

AH
Akai Haruma
Giáo viên
25 tháng 6 2024
Lời giải:
$4500=2^2.3^2.5^3$
$x< y< z$ nên $x=3$.
Khi đó: $5^3+2.5^y+5^z=4500$
$\Rightarrow 2.5^y+5^z=4375$
$5^y(2+5^{z-y})=4375=5^4.7$
Vì $2+5^{z-y}\not\vdots 5$ với mọi $y< z$ nên $5^y=5^4\Rightarrow y=4$
$\Rightarrow 2+5^{z-y}=7$
$5^{z-4}=5\Rightarrow z-4=1\Rightarrow z=5$
GL
1

29 tháng 12 2018
7z = 2x . 3y - 1 (*)
Vì x, y nguyên dương nên 2x . 3y \(⋮\) 3 \(\Rightarrow\) 2x . 3y - 1 \(\equiv\) 2 (mod 3) (1)
Ta có: 7x \(\equiv\) 1x (mod 3) \(\equiv\) 1 (mod 3) (2)
Từ (*), (1), (2) \(\Rightarrow\) Phương trình vô nghiệm
HN
0

DT
1
DL
1

13 tháng 11 2019
Ta có:
\(2^x.3^y⋮6\)
\(\Rightarrow2^x.3^y-1\) chia 6 dư - 1 (1)
Ta lại có:
\(7^z\)chia 6 dư 1 (2)
Từ (1), (2) suy ra phương trình đã cho vô nghiệm nguyên dương.
HL
0

DT
0