Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)\(\Rightarrow d:4x+5y+14=0\)
\(d':4x+5y+14=0\)
Ta có: \(\dfrac{4}{4}=\dfrac{5}{5}=\dfrac{14}{14}\) \(\Rightarrow d\equiv d'\)
b) \(\Rightarrow d:x+2y-5=0\)
Ta có: \(\dfrac{1}{2}=\dfrac{2}{4}=\dfrac{-5}{-10}\) \(\Rightarrow d\equiv d'\)
c) Ta có: \(\dfrac{1}{2}\ne\dfrac{1}{1}\) \(\Rightarrow d\) cắt \(d'\)
a/ \(\overrightarrow{AB}=\left(0;1\right)\Rightarrow\) đường thẳng AB có 1 vtpt là \(\overrightarrow{n_{AB}}=\left(1;0\right)\) và 1 vtcp là \(\overrightarrow{u_{AB}}=\left(0;1\right)\)
- Phương trình tham số AB: \(\left\{{}\begin{matrix}x=4+0.t\\y=1+1.t\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=1+t\end{matrix}\right.\)
- Phương trình tổng quát:
\(1\left(x-4\right)+0\left(y-1\right)=0\Leftrightarrow x-4=0\)
b/ Thay tọa độ x; y từ \(\Delta_1\) vào \(\Delta_2\) ta được:
\(3\left(5+i\right)-2\left(-3+2i\right)-26=0\)
\(\Leftrightarrow-i-5=0\Rightarrow i=-5\)
Thay \(i=-5\) vào pt \(\Delta_1\Rightarrow\left\{{}\begin{matrix}x=5-5=0\\y=-3+2.\left(-5\right)=-13\end{matrix}\right.\)
\(\Rightarrow\Delta_1\) cắt \(\Delta_2\) tại điểm có tọa độ \(\left(0;-13\right)\)
c/ Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|3.2-4.3+4\right|}{\sqrt{3^2+\left(-4\right)^2}}=\frac{2}{5}\)
d/ Ta có \(\overrightarrow{n_{\Delta1}}=\left(1;2\right)\) và \(\overrightarrow{n_{\Delta2}}=\left(2;-1\right)\)
\(\Rightarrow\overrightarrow{n_{\Delta1}}.\overrightarrow{n_{\Delta2}}=1.2+2.\left(-1\right)=2-2=0\)
\(\Rightarrow\Delta_1\perp\Delta_2\) hay góc giữa \(\Delta_1\) và \(\Delta_2\) bằng \(90^0\)
mk chỉ cho cách lm ; bn tự lm cho bt nha
câu a : lập bảng sét dấu tìm được \(x\) để \(y>0;y< 0\)
tiếp là đưa nó về dạng bình phương 1 số cộng 1 số \(\left(n^2+m\right)\) rồi tìm \(y_{min}\)
câu b : giao điểm của \(\left(P\right)\) và đường thẳng \(\left(d\right):y=2x+1\)
là nghiệm của hệ phương trình : \(\left\{{}\begin{matrix}y=x^2-2x-1\\y=2x+1\end{matrix}\right.\)
Bài 2:
Đường tròn \(\left(C_1\right)\) tâm \(\left(1;2\right)\) bán kính \(R=2\)
a/ Không hiểu đề bài, bạn ghi rõ thêm ra được chứ?
Tiếp tuyến đi qua giao điểm của \(\Delta_1;\Delta_2\) hay tiếp tuyến tại các giao điểm của \(\Delta_1\) và \(\Delta_2\) với đường tròn?
b/ Lại không hiểu đề nữa, điểm I trong tam giác \(IAB\) đó là điểm nào vậy bạn?
Bài 1b/
\(\Delta'\) nhận \(\left(2;1\right)\) là 1 vtpt
Gọi vtpt của d' có dạng \(\left(a;b\right)\Rightarrow\frac{\left|2a+b\right|}{\sqrt{2^2+1^2}.\sqrt{a^2+b^2}}=\frac{1}{\sqrt{2}}\)
\(\Leftrightarrow\sqrt{2}\left|2a+b\right|=\sqrt{5\left(a^2+b^2\right)}\Leftrightarrow2\left(2a+b\right)^2=5\left(a^2+b^2\right)\)
\(\Leftrightarrow3a^2+8ab-3b^2=0\Rightarrow\left[{}\begin{matrix}a=-3b\\3a=b\end{matrix}\right.\)
\(\Rightarrow\) d' có 2 vtpt thỏa mãn là \(\left(3;-1\right)\) và \(\left(1;3\right)\)
TH1: d' có pt dạng \(3x-y+c=0\)
\(d\left(I;d'\right)=R\Leftrightarrow\frac{\left|3.1-3+c\right|}{\sqrt{3^2+1^2}}=2\Rightarrow c=\pm2\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}3x-y+2\sqrt{10}=0\\3x-y-2\sqrt{10}=0\end{matrix}\right.\)
TH2: d' có dạng \(x+3y+c=0\)
\(d\left(I;d'\right)=R\Leftrightarrow\frac{\left|1+3.3+c\right|}{\sqrt{10}}=2\Leftrightarrow\left|c+10\right|=2\sqrt{10}\Rightarrow c=-10\pm2\sqrt{10}\)
\(\Rightarrow\left[{}\begin{matrix}x+3y-10+2\sqrt{10}=0\\x+3y-10-2\sqrt{10}=0\end{matrix}\right.\)
a) Xét hệ \(\left\{{}\begin{matrix}4x-10y+1=0\\x+y+2=0\end{matrix}\right.\)
D = 4.1 = 10.1 = -6 ≠ 0
Vậy d1 và d2 cắt nhau
b) Tương tự, ta có: d1 :\(12x-6y+10=0\) ;
d2= \(2x-y-7=0\)
D = 12 . (-1) - (-6).2 = -12 + 12 = 0
Dx = (-6) . (-7) - (-1). 10 = 42 + 10 = 52 ≠ 0
Vậy d1 // d2
c) Tương tự, ta có d1: \(8x+10y-12=0\)
d2:\(4x+5y-6=0\)
D = 8 . 5 - 4 . 10 = 0
Dx = 10. (-6) - (-12) . 5 = 0
Dy = (-12) . 4 - (-6) . 8 = 0
Vậy d1 trùng d2.
Xét Δ và d1, hệ phương trình: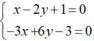
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: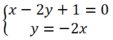
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: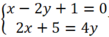
vô nghiệm
Vậy Δ // d3