Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi a, n lần lượt là lượng thức ăn 1 ngày dự kiến vá ố ngày hết thức ăn theo thực tế.
Theo dự kiến thì lượng thức ăn là 100a. Tuy nhiên, lượng thức ăn theo thực tế là
a + a 1 + 4 % + a 1 + 4 % 2 + ... + a 1 + 4 % n = a 1 + 1 , 04 + 1 , 04 2 + ... + 1 , 04 n = a 1 − 1 , 04 n 1 − 1 , 04
Yêu cầu bài toán ⇔ 100 a = a 1 − 1 , 04 n 1 − 1 , 04 ⇒ n ≈ 41

Gọi a, n lần lượt là lượng thức ăn 1 ngày dự kiến và số ngày hết thức ăn theo thực tế.
Theo dự kiến thì lượng thức ăn là 100a. Tuy nhiên, lượng thức ăn theo thực tế là


Chọn đáp án A
Gọi mức tiêu thụ dầu hàng năm của nước A theo dự báo là M.
Khí đó lượng dầu dự trữ của nước A là 100M.
Trên thực tế ta có:
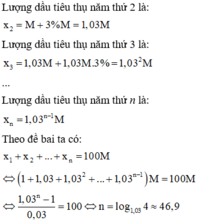

+) Gọi số ngày mà xí nghiệp đã hoàn thành công việc là x (x>0, ngày )
- Theo dự định, trong một ngày, xí nghiệp sản xuất đựoc số sản phẩm là 1500 : 30 = 50 (sản phẩm )
-Trên thực tế, trong một ngày, xí nghiệp sản xuất được số sản phẩm là 50 + 15 = 65 ( sản phẩm )
+) Theo đề bài ta có phương trình :
65x = 1500 + 255
<=> 65x = 1755
<=> x =1755 : 65 =27 (ngày )
=> Thực tế, xí nghiệp đã rút ngắn được số ngày là 30 - 27 = 3(ngày)
dự định 1 ngày làm đc : 1500 : 30 = 50sp
thực tế 1 ngày làm đc 50+15=65 sp
gọi số ngày làm thực tế là x (ngày) x>0
ta có số sp thực tế làm đc là 65x
=> 65x = 1500+255
<=> x = 27
thực tế xí nghiẹp đã rút ngắn đc 3 ngày

Chọn A.
Phương pháp:
- Gọi x x ≥ 0 (nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
- Biểu diễn các điều kiện còn lại theo x thu được hàm số ẩn x.
- Tìm GTLN của hàm số trên và kết luận.
Cách giải:
Gọi x x ≥ 0 (nghìn đồng) là số tiền tăng lên cho mỗi kg rau.
Số tiền bán mỗi một kg rau sau khi tăng là x + 30 (nghìn đồng).

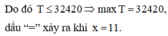
Vậy số tiền nhiều nhất bán được là 32420000 đồng.

Đáp án C
Mức giá ngôi nhà sau 10 năm bằng 10 9 1 + 5 % đồng.
Số tiền: 24.0 , 6 a + 24.0 , 6 a 1 + 10 % + 24.0 , 6 a 1 + 10 % 2
+ 24.0 , 6 a 1 + 10 % 3 + 24.0 , 6 a 1 + 10 % 4 đồng.
⇒ 24.0 , 6 a + 24.0 , 6 a 1 + 10 % + 24.0 , 6 a 1 + 10 % 2 + 24.0 , 6 a 1 + 10 % 3 + 24.0 , 6 a 1 + 10 % 4 = 10 9 1 + 5 % 5
⇔ 24.0 , 6 a 1 − 1 + 10 % 5 1 − 1 + 10 % = 10 9 1 + 5 % 5
⇒ a ≈ 14.517.000 đồng

\(1\frac{1}{3}=\frac{4}{3}\)
Phân số chỉ số hàng đã chuyển đi so với số hàng trong kho là :
\(\frac{3}{7}\cdot\frac{4}{3}=\frac{4}{7}\)(số hàng trong kho lúc đầu)
Phân số chỉ số hàng tăng lên là :
\(\frac{4}{7}-\frac{3}{7}=\frac{1}{7}\)(số hàng trong kho lúc đầu)
Số hàng trong kho lúc đầu là :
\(101:\frac{1}{7}=707\)(tấn)

Số sản phẩm bán được ở ngày 1,2,3,.... lập thành cấp số nhân với u 1 = 5 , q = 2. Theo giả thiết ta có:
![]() Tới đây ta dùng máy tính cầm tay để tìm n hoặc thay n lần lượt bằng các giá trị trong các đáp án và chọn giá trị n nhỏ nhất thỏa mãn. Chọn B.
Tới đây ta dùng máy tính cầm tay để tìm n hoặc thay n lần lượt bằng các giá trị trong các đáp án và chọn giá trị n nhỏ nhất thỏa mãn. Chọn B.

Chọn D.
Phương pháp:
Lượng thức ăn mà trang trại ăn hết ở ngày thứ k là:
Vậy thực tế lượng thức ăn dự trữ đó sẽ hết sau khoảng 43 ngày.