Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có cơ số \(a=0,3<1\) và \(3,15>\pi>\frac{2}{3}>0,5\)
Nên thứ tự tăng dần là :
\(0,3^{3,15};0,3^{\pi};0,3^{\frac{2}{3}};0,3^{0,5}\)
b) Vì số mũ \(\pi>0\) nên hàm số lũy thừa \(y=x^{\pi}\) luôn đồng biến. Mặt khác :
\(\frac{1}{\sqrt{2}}<\sqrt{2}<1,8<\pi\)
Nên thứ tự tăng dần là :
\(\left(\frac{1}{\sqrt{2}}\right)^{\pi};\sqrt{2^{\pi}};1,8^{\pi};\pi^{\pi}\)

Viết lại các số dưới dạng cùng căn bậc 6:
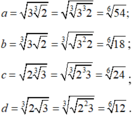
Do 12 < 18 < 24 < 54 nên d < b < c < a các số theo thứ tự tăng dần là d,b,c,a.
Chọn đáp án D.

Ta có :
\(2\log_45=\log_25\)
\(\log_{\sqrt{2}}\frac{4}{\sqrt{3}}=\log_2\frac{4}{\sqrt{3}}=\log_2\frac{16}{3}\)
\(\log_9\frac{1}{4}=\log_{3^2}\left(\frac{1}{2}\right)^2=\log_3\frac{1}{2}\)
Mà :
\(\begin{cases}\frac{1}{2}< \frac{\pi}{4}\Rightarrow\log_3\frac{1}{2}< \log_3\frac{\pi}{4}\\\log_3\frac{\pi}{4}< 0< \log_25\\5< \frac{16}{3}\Rightarrow\log_25< \log_2\frac{16}{3}\end{cases}\) \(\Rightarrow\log_3\frac{1}{2}< \log_3\frac{\pi}{4}< \log_25< \log_2\frac{16}{3}\)
Hay :
\(\log_9\frac{1}{4}< \log_3\frac{\pi}{4}< 2\log_45< \log_{\sqrt{2}}\frac{4}{\sqrt{3}}\)
Vậy thứ tự giảm dần là :
\(\log_{\sqrt{2}}\frac{4}{\sqrt{3}};2\log_45;\log_3\frac{\pi}{4};\log_9\frac{1}{4}\)
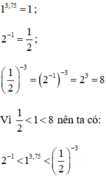


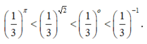
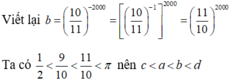
Ta có:
Vì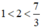 nên ta có:
nên ta có: