Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D

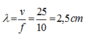
*Điều kiện về biên độ để M dao động với biên độ cực tiểu

*Xét điểm M di động trên AC ta có điều kiện về hình học.
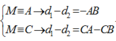
![]()
Từ (1) và (2) ta có số điểm cực tiểu trên CA:
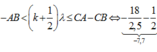
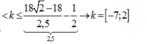
=> 10 giá trị của k tức là có 10 điểm dao động với biên độ cực tiểu.

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Bước sóng \(\lambda=\frac{v}{f}=2cm\)
Số điểm dao động với biên độ cực tiểu ứng với số giá trị của k: \(-\frac{AB}{\lambda}-0,5\le k\le\frac{AB}{\lambda}-0,5\)
\(\Leftrightarrow-5,5\le k\le4,5\)
Suy ra có 10 giá trị của k, tức là có 10 điểm dao động với biên độ cực tiểu trên AB
Đáp án C

Gọi hình chiếu của điểm M trên AB là N, trung điểm của AB là O, đặt ON = x \(\Rightarrow\) \(AM=\sqrt{4+\left(4-x\right)^2}\)\(,BM=\sqrt{4+\left(4+x\right)^2}\)
\(\vartheta BM=\frac{2\pi BM}{\lambda}\)
\(\vartheta AM=\frac{2\pi AM}{\lambda}\)
\(\Rightarrow\frac{2\pi}{\lambda}\left(MB-MA\right)=\left(2k+1\right)\lambda\pi\)
Min khi k = 0 \(\Leftrightarrow\sqrt{4+\left(4+x\right)^2}-\sqrt{4+\left(4-x\right)^2}\)\(=1\Rightarrow x\approx0,56\left(cm\right)\)
chọn đáp án A

Đáp án D
+ Bước sóng của sóng λ = v f = 2 , 5 c m
Số dãy hypebol cực tiêu trên đoạn AB là:
+ Xét tỉ số B C - A C λ = - 2 , 98 → có 10 điểm tiêu cực trên đoạn AC