

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


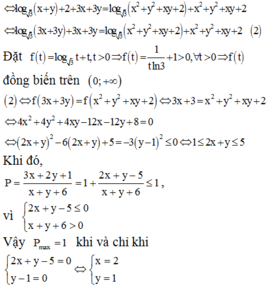

Bài này thì chia 2 vế của giả thiết cho z2 ta thu được:
\(\frac{x}{z}+2.\frac{x}{z}.\frac{y}{z}+\frac{y}{z}=4\Leftrightarrow a+2ab+b=4\)
(đặt \(a=\frac{x}{z};b=\frac{y}{z}\)).Mà ta có: \(4=a+2ab+b\le a+b+\frac{\left(a+b\right)^2}{2}\Rightarrow a+b\ge2\) Lại có:
\(P=\frac{\left(\frac{x}{z}+\frac{y}{z}\right)^2}{\left(\frac{x}{z}+\frac{y}{z}\right)^2+\left(\frac{x}{z}+\frac{y}{z}\right)}+\frac{3}{2}.\frac{1}{\left(\frac{x}{z}+\frac{y}{z}+1\right)^2}\) (chia lần lượt cả tử và mẫu của mỗi phân thức cho z2)
\(=\frac{\left(a+b\right)^2}{\left(a+b\right)^2+\left(a+b\right)}+\frac{3}{2\left(a+b+1\right)^2}\).. Tiếp tục đặt \(t=a+b\ge2\) thu được:
\(P=\frac{t}{\left(t+1\right)}+\frac{3}{2\left(t+1\right)^2}=\frac{2t\left(t+1\right)+3}{2\left(t+1\right)^2}\)\(=\frac{2t^2+2t+3}{2\left(t+1\right)^2}-\frac{5}{6}+\frac{5}{6}\)
\(=\frac{2\left(t-2\right)^2}{12\left(t+1\right)^2}+\frac{5}{6}\ge\frac{5}{6}\)
Vậy...
P/s: check xem em có tính sai chỗ nào không:v

Đặt \(x+y=t,t\in\left[-2;2\right]\)
Biến đổi được \(P=-2t^3+6t\)
Xét \(f\left(t\right)=-2t^3+6t\) trên \(\left[-2;2\right]\)
Lập bảng biến thiên
Ta có \(P_{Max}=4\) khi t=1
\(P_{Min}=-4\) khi t= -1

Nếu một trong các số \(x+y-z;y+z-x;z+x-y\) bằng 0 thì cả 3 số đều bằng 0 và dẫn đến \(x=y=z=0\), mâu thuẫn
Từ giả thiết ta có : \(\begin{cases}x\log y\left(y+z-x\right)=y\log x\left(z+x-y\right)\\y\log z\left(z+x-y\right)=z\log y\left(x+y-z\right)\\z\log x\left(x+y-z\right)=x\log z\left(y+z-x\right)\end{cases}\)
Xét đẳng thức thứ nhất ta có :
\(x\log y\left(y+z-x\right)=y\log x\left(z+x-y\right)\Leftrightarrow x\log y=y\log x.\frac{z+x-y}{y+z-x}\) \(\Leftrightarrow x\log y+y\log x=y\log x\left(\frac{z+x-y}{y+z-x}+1\right)\Leftrightarrow x\log y+z\log x=y\log x\frac{2z}{y+z-x}\)
Biến đổi tương tự với đẳng thức thứ hai ta có :
\(y\log z+z\log y=z\log y\frac{2z}{z+z-y}\)
Ta thấy rằng : \(x^y.y^x=y^z.z^y\Leftrightarrow x\log y+y\log x=y\log z+z\log y\)
Do đó ta cần có :
\(y\log x\frac{2z}{y+z-x}=z\log y\frac{2z}{z+x-y}\Leftrightarrow y\log x\left(z+x-y\right)=x\log y\left(y+z-x\right)\), đúng
Do đó ta được : \(x^yy^x=y^z.z^y\)
Chứng minh tương tự ta có : \(y^zz^y=z^x.x^z\)
=> Điều phải chứng minh

Ta có : \(P=\frac{\left(\frac{x}{y}\right)^3}{\frac{x}{y}+\frac{y}{z}}+\frac{\left(\frac{y}{z}\right)^3}{\frac{x}{y}+\frac{y}{z}}+\left(\frac{z}{x}\right)^2+\frac{15}{\frac{z}{x}}\)
Đặt \(a=\frac{x}{y};b=\frac{y}{z};c=\frac{z}{x}\Rightarrow a,b,c=1,c>1\)
Biểu thức viết lại : \(P=\frac{a^3}{a+b}+\frac{b^3}{a+b}+c^2+\frac{15}{c}\)
Ta có : \(a^3+b^3\ge ab\left(a+b\right)\Rightarrow\frac{a^3}{a+b}+\frac{b^3}{a+b}\ge ab=\frac{1}{c}\) vì a,b>0
Vậy \(P\ge\frac{1}{c}+c^2+\frac{15}{c}=c^2+\frac{16}{c}=f\left(c\right)\) với mọi \(c\in\left(1;+\infty\right)\)
Ta có \(f'\left(c\right)=2c-\frac{16}{c}\Rightarrow f'\left(c\right)=0\Leftrightarrow c=2\)
Lập bảng biến thiên ta có \(f'\left(c\right)\ge f\left(2\right)=12\) khi và chỉ khi \(c=2\Rightarrow a=b=\frac{1}{\sqrt{2}}\Rightarrow z=\sqrt{2}y=2x\)
Vậy giá trị nhỏ nhất P=12 khi và chỉ khi \(z=\sqrt{2}y=2x\)

\(P=xy-3\left(x+y\right)+9\)
Đặt \(x+y=a\Rightarrow1< a\le\sqrt{2}\)
\(a^2=x^2+y^2+2xy=1+2xy\Rightarrow xy=\frac{a^2-1}{2}\)
\(P=\frac{a^2-1}{2}-3a+9\Rightarrow2P=a^2-6a+17\)
\(2P=a^2-6a-2+6\sqrt{2}+19-6\sqrt{2}\)
\(2P=\left(a+\sqrt{2}\right)\left(a-\sqrt{2}\right)-6\left(a-\sqrt{2}\right)+19-6\sqrt{2}\)
\(2P=\left(\sqrt{2}-a\right)\left(6-\sqrt{2}-a\right)+19-6\sqrt{2}\ge19-6\sqrt{2}\)
\(\Rightarrow P\ge\frac{19-6\sqrt{2}}{2}\)
Dấu "=" xảy ra khi \(a=\sqrt{2}\) hay \(x=y=\frac{\sqrt{2}}{2}\)

\(\left(x+y\right)xy=x^2+y^2-xy\)
\(\Leftrightarrow\left(x+y\right)xy=\left(x+y\right)^2-3xy\)
Đặt \(x+y=t\Rightarrow xy=\frac{t^2}{t+3}\)
Lại có \(\left(x+y\right)^2\ge4xy\Rightarrow t^2\ge\frac{4t^2}{t+3}\)
\(\Leftrightarrow t^2\left(\frac{t-1}{t+3}\right)\ge0\Rightarrow\left[{}\begin{matrix}t\ge1\\t< -3\end{matrix}\right.\)
\(A=\frac{x^3+y^3}{\left(xy\right)^3}=\frac{\left(x+y\right)\left(x^2+y^2-xy\right)}{\left(xy\right)^3}=\frac{\left(x+y\right)\left(x+y\right)xy}{\left(xy\right)^3}=\left(\frac{x+y}{xy}\right)^2\)
\(A=\left(\frac{t\left(t+3\right)}{t^2}\right)^2=\left(\frac{t+3}{t}\right)^2=\left(1+\frac{3}{t}\right)^2\)
\(\Rightarrow y'=-\frac{6\left(t+3\right)}{t^3}< 0\) \(\forall t\ge1;t< -3\)
\(\lim\limits_{x\rightarrow-\infty}\left(1+\frac{3}{t}\right)^2=1\Rightarrow A_{max}=A\left(1\right)=16\)
\(\Rightarrow M=16\) khi \(x=y=\frac{1}{2}\)

Bạn ơi có thể hướng dẫn chi tiết giúp mình không? cám ơn nhiều ạ

Bài này cái khó là sử lý điều kiện thôi nên t làm phần đó thôi nhé.
Từ điều kiện suy ra được.
log\(\sqrt{3}\)(3x + 3y) + (3x + 3y) = log\(\sqrt{3}\)(x2 + y2 + xy + 2) + (x2 + y2 + xy + 2)
Dễ thấy hàm số f(t) = log\(\sqrt{3}\)(t) + t đồng biến trên (0; +\(\infty\)) nên
=> 3x + 3y = x2 + y2 + xy + 2