Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách thứ 2 mới đúng em nhé.
Cách 1 chỉ đúng khi dây kim loại chuyển động tịnh tiến, nhưng ở đây là dây kim loại quay quanh 1 đầu cố định.
Mình giải thích thêm về công thức trên như sau.
Ta có suất điện đọng tính bởi :
\(e=\dfrac{\Delta\phi}{\Delta t}=\dfrac{B.\Delta S}{\Delta t}=\dfrac{B.\Delta (\dfrac{\alpha}{2\pi}.\pi^2.l )}{\Delta t}=\dfrac{B.\Delta\alpha.l^{2}}{2.\Delta t}=\dfrac{B.l^{2}\omega}{2}\)
Với \(\Delta \alpha\) là góc quay trong thời gian \(\Delta t\) \(\Rightarrow \omega = \dfrac{\Delta \alpha}{\Delta t}\)
\(e_{max}\) khi \(\omega_{max}\), với \(\omega_{max}=\dfrac{v_{max}}{R}=\dfrac{\sqrt{2gl(1-\cos\alpha)}}{l}\)
Thay vào trên ta tìm đc \(e_{max}\)

- Góc lệch của dây treo VTCB:
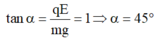
Gia tốc trong trường biểu kiến:
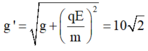
- Khi kéo lệch khỏi VTCB một góc 54° so với phương thẳng đứng thì α = 9° (góc lệch dây treo tại VTCB mới)
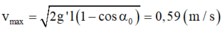

Đáp án A
Góc lệch của dây treo VTCB :
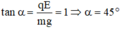
Gia tốc trong trường biểu kiến
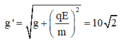
Khi kéo lệch khỏi VTCB một góc 54 ° so với phương thẳng đứng thì
![]() (góc lệch dây treo tại VTCB mới)
(góc lệch dây treo tại VTCB mới)
![]()

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)
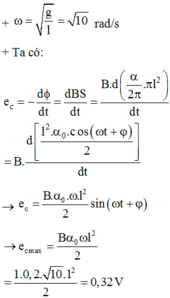
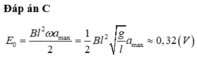
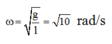
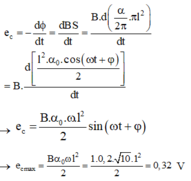

Ta có