Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Xem Hình II.5G.
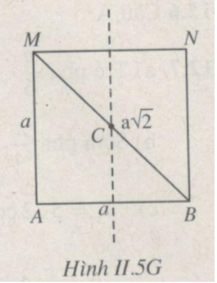
Trước hết ta tìm số vân cực đại trên toàn mặt thoáng. Đó cũng là số vân cực đại trên đoạn AB. Vì hai nguồn kết hợp dao động ngược pha nên ta có :
d 1 - d 2 = (k + 1/2) λ
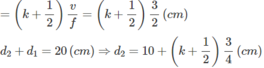
Vì 0 < d 2 < 20 (cm) ⇒ k = -13,..., -12, -1,0, 1.., 12
Bây giờ ta xét số vân cực đại trên đoạn BM.
-20 < d 2 - d 1 < 20( 2 - 1)(cm)
-20 < (k + 1/2).3/2 ≤ 2 - ( 2 - 1)
⇒ k = -13, -12 ...-1.0, 1,..., 5 ⇒ 19 điểm.

Em xem thêm lý thuyết giao thoa sóng tại đây: Giao thoa sóng | Học trực tuyến
Áp dụng công thức tổng hợp giao thoa:
\(u=2a\cos(\dfrac{\pi(d_2-d_1)}{\lambda}).\cos(\omega t -\dfrac{\pi(d_2+d_1)}{\lambda})\)
Ta có:
Câu 1:
\(\lambda = v/f=1/10=0,1m=10cm\)
M là trung điểm AB thì cách A, B là 5cm
\(\Rightarrow u=2.5\cos(\dfrac{\pi(5-5)}{10}).\cos(20\pi t -\dfrac{\pi(5+5)}{10})\)
\(\Rightarrow u=10.\cos(20\pi t -\pi)(cm)\)
Câu 2:
Bước sóng: \(\lambda = v/f = 3/5=0,6m=60cm\)
\(\Rightarrow u=2.2\cos(\dfrac{\pi(20-15)}{60}).\cos(10\pi t -\dfrac{\pi(15+20)}{60})\)
= ....

Hai điểm cách gần nhau nhất là: \(\dfrac{\lambda}{2}=10\Rightarrow \lambda=20cm\)
M O1 O2 d1 d2
M dao động cực đại và cách O2 xa nhất khi M nằm ở vân ngoài cùng về phía O1.
Vị trí vân cực đại này là: \([\dfrac{196}{2.20}]=4\)
\(\Rightarrow d_2-d_1=4.\lambda=4.20=80cm\)
\(\Rightarrow d_2= d_1+80=196+80=276cm\)
Chọn D

\(\lambda=\frac{v}{f}=\frac{1}{50}=0,2m\)
Phương trình sóng tại I là :
\(u_I=u_{I\left(A\right)}+u_{I\left(B\right)}=\left(a+b\right)\cos\left(100\pi t-\frac{AB}{2}\pi\right)\)
Lấy C thuộc MN thỏa mãn: IC = d theo thứ tự ICB với IC = d.
\(u_C=u_{C\left(A\right)}+u_{C\left(B\right)}=a\cos\left(100\pi t-\pi\left(d+\frac{AB}{2}\right)\right)+b\cos\left(100\pi t-\pi\left(\frac{AB}{2}-d\right)\right)\)
Do uC có biên độ cực đại là a+b và cùng pha với I nên u_C(A) cùng pha với u_C(B). Khi đó
\(\pi d=k2\pi\Rightarrow-5\le2k\le6,5\Rightarrow k=-2,1,0,1,2,3\)
Trong đó có cả I vậy cón 5 điểm nữa dao động cùng pha với I.
Đáp án C.
Đáp án: A
HD Giải:
λ = v/f = 1,5cm
Hai nguồn ngược pha nên điểm dao động với biên độ cực tiểu thỏa mãn: d2 – d1 = k.λ
Số điểm dao động với biên độ cực tiểu trên đoạn MB, thỏa mãn:
<=>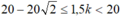
<=>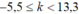
có 19 cực đại