Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Gọi A là biến cố: “ 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”
Khi đó A ¯ là biến cố :”3 sản phẩm lấy ra không có sản phẩm nào tốt”
Ta có:
Ω = C 10 3 ; Ω A = C 10 3 ⇒ P A ¯ = C 10 3 C 30 3 = 6 203
Suy ra
P A = 1 − P A ¯ = 197 203 .
Đáp án C
n Ω = C 40 3
A : ‘ 3 sản phẩm lấy ra có ít nhất 1 sản phẩm tốt ‘
A ¯ : ‘3 sản phẩm lấy ra không có sản phẩm tốt ‘
n A ¯ = C 10 3 P ( A ) = 1 − P ( A ¯ ) = 1 − C 10 3 C 40 3 = 244 247
Đáp án C
Phương pháp giải:
Chia trường hợp của biến cố, áp dụng các quy tắc đếm cơ bản tìm số phần tử của biến cố
Lời giải:
Lấy 6 sản phẩm từ 20 sản phẩm lô hàng có 
cách 
Gọi X là biến cố 6 sản phẩm lấy ra có không quá 1 phế phẩm. Khi đó, ta xét các trường hợp sau:
TH1. 6 sản phẩm lấy ra 0 có phế phẩm nào => có 
cách
TH2. 6 sản phẩm lấy ra có duy nhất 1 phế phẩm => có 
cách
Suy ra số kết quả thuận lợi cho biến cố X là 
Vậy xác suất cần tính là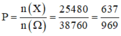 
hoành độ giao điểm là nghiệm của pt
\(x^3+3x^2+mx+1=1\Leftrightarrow x\left(x^2+3x+m\right)=0\)
\(x=0;x^2+3x+m=0\)(*)
để (C) cắt y=1 tại 3 điểm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 0
\(\Delta=3^2-4m>0\) và \(0+m.0+m\ne0\Leftrightarrow m\ne0\)
từ pt (*) ta suy ra đc hoành độ của D, E là nghiệm của (*)
ta tính \(y'=3x^2+6x+m\)
vì tiếp tuyến tại Dvà E vuông góc
suy ra \(y'\left(x_D\right).y'\left(x_E\right)=-1\)
giải pt đối chiếu với đk suy ra đc đk của m
Số sản phẩm bán được ở ngày 1,2,3,.... lập thành cấp số nhân với u 1 = 5 , q = 2. Theo giả thiết ta có:
Tới đây ta dùng máy tính cầm tay để tìm n hoặc thay n lần lượt bằng các giá trị trong các đáp án và chọn giá trị n nhỏ nhất thỏa mãn. Chọn B.
hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm
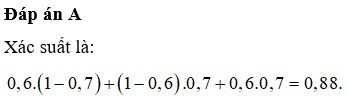
Đáp án A
Lô 1 : Xác suất lấy sản phẩm tốt : 0,6
Xác suất lấy sản phẩm không tốt : 0,4
Lô 2 : Xác suất lấy sản phẩm tốt :0,7
Xác suất lấy sản phẩm không tốt : 0,3
⇒ xác suất để trong hai sản phẩm lấy ra có ít nhất một sản phẩm có chất lượng tốt :
p = 0 , 6.0 , 7 + 0 , 6.0 , 3 + 0 , 7.0 , 4 = 0 , 88