
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

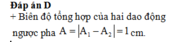

Biên độ dao động tổng hợp thỏa mãn: \(\left|A_1-A_2\right|\le A\le\left|A_1+A_2\right|\)
\(\Rightarrow\) A = 5 (cm) thỏa mãn hệ thức

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Tổng quãng đường vật đi được trong 1 chu kì là: \(5+5+18=28cm\)
Trong 1 chu kì vật đi được quãng đường là 4A
\(\Rightarrow 4A = 28\)
\(\Rightarrow A = 7cm\)

Áp dụng: \(v_{max}= \omega A \Rightarrow \omega = \frac{v_{max}}{A} = \frac{10\pi}{5} = 2\pi \ (rad/s)\)
\(\Rightarrow T = \frac{2\pi}{\omega} = 1 s\)

Phương trình tổng quát: \(x = Acos(\omega t +\varphi)\)
+ \(\omega = 2\pi f = 2\pi .10 = 20\pi \ (rad/s) \)
+ A = 4cm.
+ t = 0, vật qua x0 = A \(\Rightarrow\left\{ \begin{array}{} x_0 = 4\ cm\\ v_0 =0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 1\ cm\\ \sin \varphi = 0 \end{array} \right. \Rightarrow \varphi = 0\)
Vậy phương trình dao động: \(x = 4\cos(20\pi t) \ (cm)\)

Lực kéo về
\(F = -kx= -k.A.\cos (\omega t +\varphi)\)
So sánh với phương trình \(F=-0.8\cos 4t(N)\) => \(\omega = 4\)(rad/s) và \( k.A = 0,8 \)
\(=> m\omega^2 A = 0,8 => A = \frac{0,8}{m\omega^2}= \frac{0,8}{0,5.4^2}= 0,1 m = 10cm.\)