Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình dao động của hai chất điểm :
x 1 = A cos ( ω t - π 2 ) và x 2 = A cos ( ω 2 t - π 2 )
Mặc khác v 2 m a x = A ω 2 ⇒ ω = π r a d / s
Hai chất điểm này gặp nhau
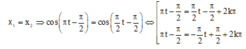
+ Với nghiệm thứ nhất ⇒ t 1 = 4
+ Với nghiệm thứ hai ⇒ t 2 = 2 3 ( 2 k + 1 )
Các thời điểm gặp nhau
| t 1 |
0 |
4 |
8 |
16 |
… |
| t 2 |
0,67 |
2 |
3,83 |
4,67 |
… |
a lần gặp thứ 5 ứng với t=4,67s

Đáp án B

Từ thời điểm t o đến t 1 :
+ Vectơ biểu diễn dao động của B quay góc B: ![]()
+ Vectơ biểu diễn dao động của C quay góc C: ![]()
Ta có: 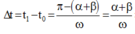
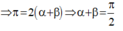
+ Mà: 
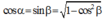

+ Vectơ biểu diễn dao động của D đang từ VTCB cũng quay góc π 2 giống như B và C nên tới vị trí biên.
+ Đến thời điểm t 2 vectơ biểu diễn dao động của D quay thêm góc:


Đáp án C
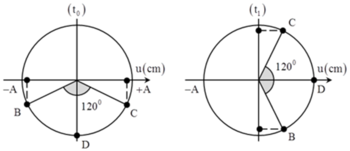
+ Biểu diễnn các vị trí tương ứng, tại các thời điểm trên đường tròn.
Với góc α luôn không đổi và sin α 2 = v t 1 v m a x = 3 2 ⇒ α = 120 0 .
=> Từ hình vẽ, ta có 3 2 A = 5 3 ⇒ A = 10 m m .

Đáp án B
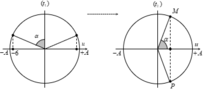
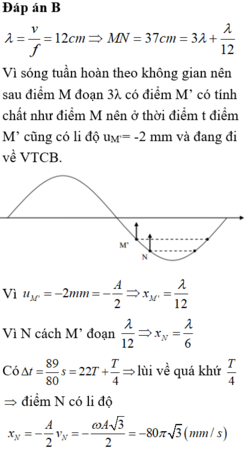
Ta có : λ = v f = 12 cm ⇒ MN = 37 cm = 3 λ + λ 12
Vì sóng tuần hoàn theo không gian nên sau điểm M đoạn 3λ có điểm M’ có tính chất như điểm M nên ở thời điểm t điểm M’ cũng có li độ uM’= -2 mm và đang đi về VTCB.
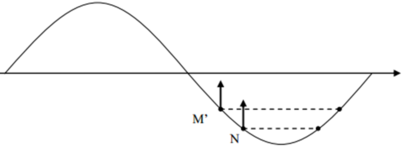
Vì uM’ = –2mm = –A/2 => xM’ = λ/12
Vì N cách M’ đoạn λ/12 => xN = λ/6.
Ta có : ∆ t = 89 80 s = 22 T + T 4 ⇒ lùi về quá khứ T 4
=> điểm N có li độ xN = –A/2
v N = - ωA 3 2 = - 80 π 3 ( mm / s ) .

Hướng dẫn: Chọn đáp án B
Hai phần tử gần nhau nhất có độ lớn li độ A/2 chuyển động ngược chiều nhau cách nhau d = λ /3 = 8 cm ⇒ λ = 24 cm . Tốc độ truyền sóng trên dây và tốc độ dao động cực đại của phần tử trên dây lần lượt là :
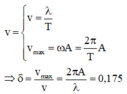

x 4,8 -4,8 O A B C x O A B C 5,5 H1 H2 H
Ta có giản đồ véc tơ ở thời điểm t1 và t2 như hình vẽ.
Do các véc tơ quay ngược chiều kim đồng hồ với tốc độ như nhau nên tam giác AOC không thay đổi hình dạng.
Ở H1: AC = 4,8 . 2 = 9,6 mm.
Ở H2: AH = AC/ 2 = 4,8 mm.
Tam giác AOH có: \(OA^2=\sqrt{OH^2+AH^2}=\sqrt{5,5^2+4,8^2}=7,3\)mm
Vào thời điểm t2, B đang ở biên nên có li độ là 7,3mm.