Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương trình dao động của hai chất điểm :
x 1 = A cos ( ω t - π 2 ) và x 2 = A cos ( ω 2 t - π 2 )
Mặc khác v 2 m a x = A ω 2 ⇒ ω = π r a d / s
Hai chất điểm này gặp nhau
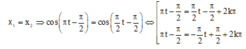
+ Với nghiệm thứ nhất ⇒ t 1 = 4
+ Với nghiệm thứ hai ⇒ t 2 = 2 3 ( 2 k + 1 )
Các thời điểm gặp nhau
| t 1 |
0 |
4 |
8 |
16 |
… |
| t 2 |
0,67 |
2 |
3,83 |
4,67 |
… |
a lần gặp thứ 5 ứng với t=4,67s

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Đáp án B

Từ thời điểm t o đến t 1 :
+ Vectơ biểu diễn dao động của B quay góc B: ![]()
+ Vectơ biểu diễn dao động của C quay góc C: ![]()
Ta có: 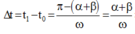
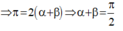
+ Mà: 
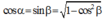

+ Vectơ biểu diễn dao động của D đang từ VTCB cũng quay góc π 2 giống như B và C nên tới vị trí biên.
+ Đến thời điểm t 2 vectơ biểu diễn dao động của D quay thêm góc:


\(E=\frac{1}{2}\omega^2A^2\) nên vận tốc truyền sóng không ảnh hưởng.
chọn D

Hướng dẫn: Chọn đáp án B
Hai phần tử gần nhau nhất có độ lớn li độ A/2 chuyển động ngược chiều nhau cách nhau d = λ /3 = 8 cm ⇒ λ = 24 cm . Tốc độ truyền sóng trên dây và tốc độ dao động cực đại của phần tử trên dây lần lượt là :
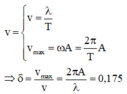

Đáp án B
+ Ta biểu diễn dao động của hai phần tử dây cùng có li độ + 4 mm nhưng chuyển động ngược chiều nhau trên đường tròn.
→ Từ hình vẽ, ta có
∆ φ = 2 πd λ = 2 π 3 ⇒ λ = 3 d = 3 . 8 = 24 cm .
+ Tỉ số δ = ωA v = 2 πA λ = 2 π . 0 , 8 24 = 0 , 21 .




Đáp án C
+ Biểu diễnn các vị trí tương ứng, tại các thời điểm trên đường tròn.
Với góc α luôn không đổi và sin α 2 = v t 1 v m a x = 3 2 ⇒ α = 120 0 .
=> Từ hình vẽ, ta có 3 2 A = 5 3 ⇒ A = 10 m m .