Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi H(x;y) là điểm thuộc tia phân giác của 2 đường thẳng 3x-4y+12=0(d1) va 12x+5y-7=0(d2)
\(\Rightarrow\) d(H;d1) = d(H;d2) \(\Leftrightarrow\dfrac{\left|3x-4y+12\right|}{\sqrt{3^2+\left(-4\right)^2}}=\dfrac{\left|12x+5y-7\right|}{\sqrt{12^2+5^2}}\Leftrightarrow\)
\(13\left(3x-4y+12\right)=\pm5\left(12x+5y-7\right)\)vậy pt 2 đường phân giác là:
\(\Leftrightarrow\left[{}\begin{matrix}21x+77y-192=0\\99x-27y+121=0\end{matrix}\right.\)

Cho 2 đường thẳng cắt nhau d 1 : a 1 x + b 1 y + c 1 = 0 v à d 2 : a 2 x + b 2 y + c 2 = 0 .
Khi đó, phương trình đường phân giác tạo bởi 2 đường thẳng là:
a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = ± a 2 x + b 2 y + c 2 a 2 2 + b 2 2
Áp dụng công thức ta có phương trình hai phân giác là:
3 x − 4 y + 1 3 2 + ( − 4 ) 2 = ± x + 3 1 2 + 0 2 ⇔ 3 x − 4 y + 1 5 = ± ( x + 3 ) ⇔ 3 x − 4 y + 1 = ± 5 x + 3 ⇔ 2 x + 4 y + 14 = 0 8 x − 4 y + 16 = 0 ⇔ x + 2 y + 7 = 0 2 x − y + 4 = 0
ĐÁP ÁN C

Giả sử: \(d_{\left(M,\Delta_1\right)}=d_{\left(M,\Delta_2\right)}\)
\(\Rightarrow\dfrac{\left|2x+4y+7\right|}{\sqrt{2^2+4^2}}=\dfrac{\left|x-2y-3\right|}{\sqrt{1^2+2^2}}\)
\(\Rightarrow\sqrt{5}\left|2x+4y+7\right|=2\sqrt{5}\left|x-2y-3\right|\)
\(\Rightarrow\left|2x+4y+7\right|=2\left|x-2y-3\right|\)
* \(2x+4y+7=2\left(x-2y-3\right)\)
\(\Rightarrow8y+13=0\)
*\(2x+4y+7=-2\left(x-2y-3\right)\)
\(\Rightarrow4x+1=0\)

Đáp án B
Ta có: ![]() là véc tơ pháp tuyến của d; d’ và
là véc tơ pháp tuyến của d; d’ và ![]()
Nên phương tình đường phân giác của góc nhọn là:
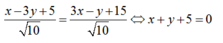

Phương trình các đường phân giác của các góc tạo bởi d và d’ là:
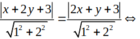
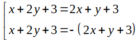
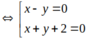
Chọn C.

Chọn C.
Các đường phân giác của các góc tạo bởi d và d' có phương trình:
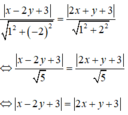
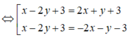
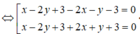
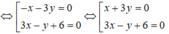

AB giao AH \(\Rightarrow A=\left\{{}\begin{matrix}x-3y+11=0\\3x+7y-15=0\end{matrix}\right.\)
\(\Rightarrow A\left(-2;3\right)\)
AB giao BH \(\Rightarrow B=\left\{{}\begin{matrix}x-3y+11=0\\3x-5y+13=0\end{matrix}\right.\)
\(\Rightarrow B\left(4;5\right)\)
*\(AH\perp BC\Rightarrow BC:7x-3y+a=0\)
Mà BC đi qua B \(\Rightarrow7\times4-3\times5+c=0\Rightarrow c=-13\)
BC: \(7x-3y-13=0\)
*\(BH\perp AC\Rightarrow AC:5x+3y+c=0\)
Mà AC đi qua A \(\Rightarrow5\times\left(-2\right)+3\times3+c=0\Rightarrow c=1\)
AC: \(5x+3y+1=0\)

Cho 2 đường thẳng cắt nhau d 1 : a 1 x + b 1 y + c 1 = 0 v à d 2 : a 2 x + b 2 y + c 2 = 0 .
Lấy điểm M(x, y) bất kì trên đường phân giác của góc tạo bởi 2 đường thẳng d1; d2.
Theo tính chất đường phân giác của góc ta có:
d ( M ; d 1 ) = d ( M ; d 2 ) ⇔ a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = a 2 x + b 2 y + c 2 a 2 2 + b 2 2 ⇔ a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = ± a 2 x + b 2 y + c 2 a 2 2 + b 2 2
ĐÁP ÁN B
Gọi M(x;y) là điểm thuộc đường phân giác của góc tạo bởi hai đường thẳng đã cho
+) Ta có:
+) Do điểm M thuộc đường phân giác của góc tạo bởi hai đường thẳng d1 và d2 nên điểm M cách đều hai đường thẳng trên: d( M; d1)= d(M, d2 )
Vậy phương trình 2 đường phân giác của góc tạo bởi hai đường thẳng đã cho là:
-21 x – 77y + 191= 0 và 99x – 27y + 121 =0