Làm tính trừ phân thức: x + 9...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

13 tháng 12 2018

Làm tính trừ phân thức: x + 9 x 2 - 9 - 3 x 2 + 3 x

1

CM

Cao Minh Tâm

13 tháng 12 2018

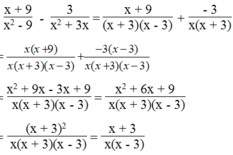
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Các câu hỏi dưới đây có thể giống với câu hỏi trên

YN

Yến Nhi

1 tháng 11 2016 - olm

thực hiện phép trừ phân thức không cùng mẫu:

a/\(\frac{8+9}{x^2-9}-\frac{3}{x^2+3x}\) b/ \(\frac{18}{\left(x-3\right)\left(x^2-9\right)}-\frac{3}{x^2-6x+9}-\frac{x}{x^2-9}\)

0

MN

my name is crazy

8 tháng 8 2018 - olm

Trừ phân thức

a) \(\frac{1}{3x-2}-\frac{1}{3x+2}-\frac{3x-6}{4-9x^2}\)

b) \(\frac{18}{\left(x-3\right)\left(x^2-9\right)}-\frac{3}{x^2-6x+9}-\frac{x^2}{x^2-9}\)

1

TN

Thanh Ngân

8 tháng 8 2018

\(\frac{1}{3x-2}-\frac{1}{3x+2}-\frac{3x-6}{4-9x^2}\)

\(=\frac{3x+2}{9x^2-4}-\frac{3x-2}{9x^2-4}+\frac{3x-6}{9x^2-4}\)

\(=\frac{3x+2-3x+2+3x-6}{9x^2-4}\)

\(=\frac{3x-2}{9x^2-4}\)

\(=\frac{1}{3x+2}\)

\(\frac{18}{\left(x-3\right)\left(x^2-9\right)}-\frac{3}{x^2-6x+9}-\frac{x^2}{x^2-9}\)

\(=\frac{18}{\left(x-3\right)\left(x-3\right)\left(x+3\right)}\) \(-\frac{3\left(x+3\right)}{\left(x-3\right)\left(x-3\right)\left(x+3\right)}\)\(-\frac{x^2\left(x-3\right)}{\left(x-3\right)\left(x+3\right)\left(x-3\right)}\)

\(=\frac{18-3x-9-x^3+3x^2}{\left(x-3\right)^2\left(x+3\right)}\)

\(=\frac{-x^3+3x^2-3x+9}{\left(x-3^2\right)\left(x+3\right)}\)

\(=\frac{\left(-x^2-3\right)\left(x-3\right)}{\left(x-3^2\right)\left(x+3\right)}\)

\(=\frac{-x^2-3}{\left(x-3\right)\left(x+3\right)}\)

học tốt

SG

Sách Giáo Khoa

28 tháng 4 2017

Làm tính trừ phân thức...

1

NT

Nguyen Thuy Hoa

28 tháng 6 2017

Phép trừ các phân thức đại số

TL

Trần Lê Huy

12 tháng 11 2016 - olm

tính chất của phân thức đại số : \(\frac{A}{B}=\frac{-A}{-B}\)Cô ơi nhưng trong ví dụ này em áp dụng tính chất này lại làm sai ạ ? Cô ơi cô giải thích giúp em nhe cô. Em cám ơn cô :)Đề bài: em xét xem ví dụ về phân thức bằng nhau này đúng không ?\(\frac{\left(x-9\right)^3}{2\left(9-x\right)}=\frac{\left(9-x\right)^2}{2}\)giải: \(VT=\frac{\left(x-9\right)^3}{2\left(9-x\right)}=-\frac{-\left(9-x\right)^3}{< !>2\left(9-x\right)<...

3

CW

Cold Wind

12 tháng 11 2016

<!> là gì vậy ak?

BV

bolyl vc dtntsp

12 tháng 11 2016

tôi nghĩ là giao thừa

SG

Sách Giáo Khoa

28 tháng 4 2017

Biến đổi mỗi phân thức sau thành phân thức có mẫu thức là \(x^2-9\)

\(\dfrac{3x}{x+3};\dfrac{x-1}{x-3};x^2+9\)

1

DD

Đinh Đức Hùng

29 tháng 4 2017

\(\dfrac{3x}{x+3}=\dfrac{3x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3x^2-9x}{x^2-9}\)

\(\dfrac{x-1}{x-3}=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2+2x-3}{x^2-9}\)

\(x^2+9=\dfrac{\left(x^2+9\right)\left(x^2-9\right)}{x^2-9}=\dfrac{x^4-81}{x^2-9}\)

PT

Phạm Thị Thắm Phạm

13 tháng 4 2019 - olm

Bài 1: Cho biểu thức: A=\(\left(\frac{3-x}{x+3}.\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\) a) Rút gọn biểu thức A b) TÍnh giá trị biểu thức A, với x=\(\frac{-1}{2}\) c) Tìm giá trị của x để A<0Bài 2: Cho phân thức \(\frac{2x^2-4x+8}{x^3+8}\) a) Với điều kiện nào của x thì giá trị của phân thức xác định b) Hãy rút gọn phân thức c) Tính giá trị của phân thức tại x=2 ...

1

TT

Trần Thị Ngọc Ánh

13 tháng 4 2019

bài1 A=\(\left(\frac{3-x}{x+3}\cdot\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

=\(\left(-\frac{x-3\cdot\left(x+3\right)^2}{\left(x+3\right)^2\cdot\left(x-3\right)}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

=\(-\frac{x}{x+3}\cdot\frac{x+3}{3x^2}=\frac{-1}{3x}\)

b) thế \(x=-\frac{1}{2}\)vào biểu thức A

\(-\frac{1}{3\cdot\left(-\frac{1}{2}\right)}=\frac{2}{3}\)

c) A=\(-\frac{1}{3x}< 0\)

VÌ (-1) <0 nên 3x>0

x >0

BV

ba vu

19 tháng 12 2022

câu 3 phân thức nghịch đảo của phân thức 2/x-4v(với x≠4)

câu 4 phân thức 2/ x-3 không có nghĩa khi

câu 5 rút gọn phân thức x-3/ x^2-9 ( với x≠ cộng trừ 3) ta được kết quả

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 12 2022

Câu 4: Không có nghĩa khi x-3=0

=>x=3

Câu 5:

\(A=\dfrac{x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)

SG

Sách Giáo Khoa

28 tháng 4 2017

Theo định nghĩa của phép trừ, khi viết :

\(\dfrac{A}{B}-\dfrac{C}{D}-\dfrac{E}{F}\) có nghĩa là \(\dfrac{A}{B}+\dfrac{-C}{D}+\dfrac{-E}{F}\)

Áp dụng điều này để làm các phép tính sau :

a) \(\dfrac{1}{3x-2}-\dfrac{1}{3x+2}-\dfrac{3x-6}{4-9x^2}\)

b) \(\dfrac{18}{\left(x-3\right)\left(x^2-9\right)}-\dfrac{3}{x^2-6x+9}-\dfrac{x}{x^2-9}\)

1

NT

Nguyen Thuy Hoa

28 tháng 6 2017

Phép trừ các phân thức đại số

Phép trừ các phân thức đại số

SG

Sách Giáo Khoa

27 tháng 4 2017

Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau :

a) \(\dfrac{x^2y^3}{5}=\dfrac{7x^3y^4}{35xy}\)

b) \(\dfrac{x^2\left(x+2\right)}{x\left(x+2\right)^2}=\dfrac{x}{x+2}\)

c) \(\dfrac{3-x}{3+x}=\dfrac{x^2-6x+9}{9-x^2}\)

d) \(\dfrac{x^3-4x}{10-5x}=\dfrac{-x^2-2x}{5}\)

1

A

ÁcΦ┼Quỷ♪

7 tháng 5 2017

a. \(x^2y^3.35xy=5.7x^3y^4\)

\(\Leftrightarrow35x^3y^4=35x^3y^4\Rightarrowđpcm\)

\(b.x^2\left(x+2\right).\left(x+2\right)=x\left(x+2\right)^2.x\)

\(\Leftrightarrow x^2\left(x+2\right)^2=x^2\left(x+2\right)^2\Rightarrowđpcm\)

\(c.\left(3-x\right)\left(9-x^2\right)=\left(3+x\right)\left(x^2-6x+9\right)\)

\(\Leftrightarrow\left(3-x\right)\left(3-x\right)\left(3+x\right)=\left(3+x\right)\left(3-x\right)^2\)

\(\Leftrightarrow\left(3-x\right)^2\left(3+x\right)=\left(3-x\right)^2\left(3+x\right)\)

\(\Rightarrowđpcm\)

\(d.5\left(x^3-4x\right)=\left(10-5x\right)\left(-x^2-2x\right)\)

\(\Leftrightarrow5x^3-20x=5x^3-20x\Rightarrowđpcm\)

TD

Trọng Đặng Đình

10 tháng 2 2018 - olm

Ai giúp bài này gấp với

Cho biểu thức : A= \(\left(\frac{3-x}{x+3}.\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

a, Rút gọn biểu thức A

b, Tính giá trị của bểu thức A , với x=\(-\frac{1}{2}\)

c,Tính giá trị của x để A < 0

2

NX

Nguyễn Xuân Anh

10 tháng 2 2018

\(\text{a, ĐKXĐ: }\hept{\begin{cases}x+3\ne0\\x-3\ne0\\3x^2\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne\mp3\\x\ne0\end{cases}}\)

\(A=\left(\frac{3-x}{x+3}\cdot\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

\(=\left[\frac{\left(3-x\right)\left(x+3\right)^2}{\left(x+3\right)\left(x+3\right)\left(x-3\right)}+\frac{x}{x+3}\right]\cdot\frac{x+3}{3x^2}\)

\(=\frac{x-x-3}{x+3}\cdot\frac{x+3}{3x^2}\)

\(=-\frac{1}{x^2}\)

b, với x=\(-\frac{1}{2}\)ta có:

\(A=-\frac{1}{\left(-\frac{1}{2}\right)^2}=-4\)

c, Để A<0 thì \(-\frac{1}{x^2}< 0\text{ mà }x^2>0\left(\text{vì x khác 0 ĐKXĐ}\right)\)

Với x khác 0 thì thỏa mãn!

KT

Không Tên

10 tháng 2 2018

a) ĐKXĐ: \(x\ne\pm3\)

\(A=\left(\frac{3-x}{x+3}.\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

\(=\left(\frac{3-x}{x+3}.\frac{\left(x+3\right)^2}{\left(x-3\right)\left(x+3\right)}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

\(=\left(\frac{3-x}{x-3}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)

\(=\frac{\left(3-x\right)\left(x+3\right)+x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}.\frac{x+3}{3x^2}\)

\(=\frac{3\left(3-x\right)}{\left(x-3\right)\left(x+3\right)}.\frac{x+3}{3x^2}\)

\(=-\frac{1}{x^2}\)