Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AIKD có
AI//KD
AI=KD
AI=AD
=>AIKD là hình thoi
mà góc A=90 độ
nên AIKD là hình vuông
Xét tứ giác BIKC có
BI//KC
BI=KC
BI=BC
=>BIKC là hình thoi
mà góc B=90 độ
nên BIKC là hình vuông
b: Xét ΔDIC có
IK vừa là đường cao, vừa là trung tuyến
IK=1/2DC
Do đó: ΔDIC vuông cân tại I
c: AIKD là hình vuông
=>AK vuông góc ID tại trung điểm của mỗi đường và AK=ID
=>AK=ID và AK vuông góc ID tại S
=>SI=SK
BIKC là hình vuông
=>CI vuông góc BK tại trung điểm của mỗi đường và CI=BK
=>CI vuông góc BK tại R
=>RI=RC=RK=RB
Xét tứ giác ISKR có
góc ISK=góc IRK=góc SIK=90 độ
Do đó: ISKR là hình chữ nhật
mà SI=SK
nên ISKR là hình vuông

a/ Ta có
AB=BC và MA=MB; NB=NC => MB=NC
Xét hai tg vuông BMC và tg vuông CNC có
MB=NC (cmt)
BC=CD (cạnh hình vuông)
=> tg BMC= tg CND => ^BMC=^CND (1)
Trong tg vuông BMC có ^BCM+^BMC=90 (2)
Từ (1) và (2) => ^BCM+^CND=90 => ^CHN=90 => MC vuông góc DN
b/
Ta có AB=CD (cạnh hình vuông) và MA=MB; KC=KD => MA=KC
Mà MA//KC
=> AMCK là hình bình hành => AK//MC (3)
Xét tg CDH có ID=IH và KD=KC (đề bài) => IK là đường trung bình => IK//MC (4)
Từ (3) và (4) => AK trùng với IK => A; I; K thẳng hàng
c/
Xét tg ADH có
AI//MC mà MC vuông góc với DN => AI vuông góc với DN => AI là đường cso của tg ADH (5)
Ta có ID=IH (đề bài) => AI là trung tuyến của tg ADH (6)
Từ (5) và (6) => tg ADH cân tại A (tam giác có đường cao đồng thời là đường trung tuyến ... là tam giác cân)

a: Xét tứ giác BIKC có
BI//KC
BI=KC
Do đó: BIKC là hình bình hành
mà \(\widehat{B}=90^0\)
nên BIKC là hình chữ nhật

A B C D N M
a) Ta có :
AB // CD ( Vì ABCD là hcn )
mà N \(\in\) AB
M \(\in\) DC
=) AN // MD
Xét hcn ABCD có :
M là tđ của cạnh DC
NA // MD
=) N là tđ của AB
=) NA = NB
mà AM = MC
lại có : AB = DC ( vì ABCD là hcn )
=) AN = DM
mà AN // DM
=) ANMD là hbh
mà góc M = 90o
=) ANMD là hcn
b)
Ta có : AN = MC ( Vì cx = MD )
mà AN // DC
=) ANCM là hbh
câu c) chút nữa mình làm bn vẽ hình trước
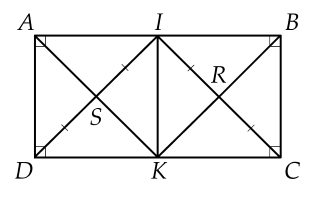
a) Vì ��=2��AB=2BC suy ra ��=��2=��BC= AB/2=AD
ABCD là hình chữ nhật nên AB=DC suy ra 1/2AB=1/2DC do đó AI=DK=AD
Tứ giác AIKD có AI//DK, AI=DK nên tứ giác AIKD là hình bình hành
Lại có AD=AI nên AIKD là hình thoi
Mà góc IAD= 90 độ do đó AIKD là hình vuông
Vậy tứ giác AIKD là hình vuông
Chứng minh tương tự cho tứ giác BIKC
Vậy tứ gáic BIKC là hình vuông
b) VÌ AIKD là hình vuông nên DI là tia phân giác góc ADK nên góc IDK = 45 độ
Tương tự góc ICK = 45 độ
Tam giác IDC cân có góc DIC = 90 độ nên là tam gaic vuông cân
Vậy tam giác IDC là tam gáic vuông cân
c) Vì AIKD, BCKI là các hình vuông nên hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường nên SI=SK=DI/2 và IR=RK=IC/2
=>ISKR là hình thoi
Lại có góc DIC= 90 độ nên ISKR là hình vuông
Vậy ISKR là hình vuông