Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu hàm số y = f(x) liên tục trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0 có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- f ( x ) = x 2 − 1 liên tục trên đoạn [−2;2], f(−2).f(2) = 9 > 0
Phương trình x 2 – 1 = 0 có nghiệm x = 1 hoặc x = -1 trong khoảng (-2; 2)
- f ( x ) = x 2 + 1 liên tục trên đoạn [-1; 1] và f(−1).f(1) = 4 > 0. Còn phương trình x 2 + 1 = 0 lại vô nghiệm trong khoảng (-1; 1)

\(a=-2b-5c\Rightarrow a+2b=-5c\)
- Với \(c=0\Rightarrow a=-2b\Rightarrow-\dfrac{b}{a}=\dfrac{1}{2}\)
\(ax^2+bx=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{b}{a}=\dfrac{1}{2}\in\left(0;1\right)\end{matrix}\right.\) (thỏa mãn)
- Với \(c\ne0\)
Hàm \(f\left(x\right)=ax^2+bx+c\) liên tục trên R
\(f\left(0\right)=c\) ;
\(f\left(\dfrac{1}{2}\right)=\dfrac{a}{4}+\dfrac{b}{2}+c=\dfrac{a+2b+4c}{4}=\dfrac{-5c+4c}{4}=-\dfrac{c}{4}\)
\(\Rightarrow f\left(0\right).f\left(\dfrac{1}{2}\right)=-\dfrac{c^2}{4}< 0;\forall c\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;\dfrac{1}{2}\right)\Rightarrow f\left(x\right)\) có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) do \(\left(0;\dfrac{1}{2}\right)\subset\left(0;1\right)\)


Ta có:
y = f(x) là hàm số đa thức liên tục trên R.
Do đó f(x)liên tục trên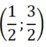
Từ đó suy ra, phương trình f(x) = 0 có ít nhất một nghiệm xo ∈ (0;2)