Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài cạnh thứ ba của tam giác là x cm (x > 0)
Áp dụng bất đẳng thức trong tam giác ta có: 10 – 2 < x < 10 + 2
Hay 8 < x < 12
Trong bốn đáp án A, B, C, D thì đáp án D thỏa mãn vì 8 < 9 < 12
Vậy độ dài cạnh thứ ba là 9 cm.
Chọn đáp án D

Gọi cạnh còn lại có độ dài là \(x\), theo bất đẳng thức tam giác ta có:
\(7-1< x< 7+1\Rightarrow6< x< 8\)
⇒ \(x=7\)
Chọn D
Gọi độ dài cạnh còn lại của tam giác là `x (x \ne 0,`\(\in N\)\(\text{*}\) `)`
Theo bất đẳng thức tam giác ta có:
`1+7 > x > 7-1`
`-> 8> x> 6`
`-> x= {7}`
Xét các đáp án `-> D (tm)`

a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
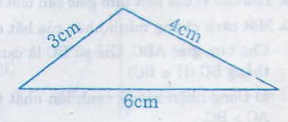
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
a) Nhận xét: 2cm + 3cm = 5cm < 6cm nên bộ ba đoạn thẳng dài 2cm, 3cm, 6cm không phải là bộ ba cạnh của một tam giác.
b) Nhận xét: 2cm + 4cm = 6cm = 6cm nên bộ ba đoạn thẳng dài 2cm, 4cm, 6cm không phải là bộ ba cạnh của một tam giác.
c) Nhận xét: 3cm + 4cm = 7cm > 6cm nên bộ ba đoạn thẳng dài 3cm, 4cm, 6cm là bộ ba cạnh của một tam giác.


Ngày mai mình nộp bài rồi, mong các bạn chỉ bài giúp mình . mình không hiểu gì về 2 bài toán này cả TT_TT

gọi các cạnh của tam giác lần lượt là a,b,c .
Theo bài ra : a + b + c = 64 và a,b,c tỉ lệ thuận với 3,6,7
\(\Rightarrow\frac{a}{3}=\frac{b}{6}=\frac{c}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có :
\(\frac{a}{3}=\frac{b}{6}=\frac{c}{7}=\frac{a+b+c}{3+6+7}=\frac{64}{16}=4\)
\(\Rightarrow a=12;b=24;c=28\)
Vậy ...
Gọi a, b, c lần lượt là các cạnh của tam giác đó. Mà a, b, c tỉ lệ thuận với 3, 6, 7 => \(\frac{a}{3}=\frac{b}{6}=\frac{c}{7}\)
Mà chu vi của tam giác đó là 64 cm => a+b+c = 64
Áp dụng tính chất của dãy tỉ số bằng nhau
\(\frac{a}{3}=\frac{b}{6}=\frac{c}{7}=\frac{a+b+c}{3+6+7}=\frac{64}{16}=4\)
\(\frac{a}{3}\)=4 => a = 3.4=12
\(\frac{b}{6}\)= 4 => b = 6.4 = 24
\(\frac{c}{7}\)= 4 => c = 7.4 = 28
Vậy a = 12 , b=24 , c = 28
Chọn D