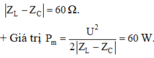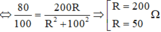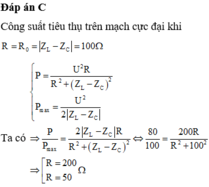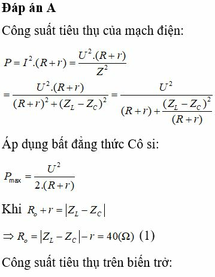Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
+ Công suất tiêu thụ trên mạch cực đại khi R = R 0 = Z L - Z C = 100 Ω .
Lập tỉ số:
P = U 2 R R 2 + Z L - Z C 2 P max = U 2 2 Z L - Z C ⇒ P P max = 2 Z L - Z C R R 2 + Z L - Z C 2 ⇔ 80 100 = 200 R R 2 + 100 2 ⇒ R = 200 R = 50 Ω .

Dung kháng của tụ là \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \).

\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Đáp án B
+ Giá trị của R để công suất tiêu thụ trên mạch cực đại là:
![]()
+ Giá trị của R để công suất trên biến trở là cực đại
![]()
Từ hai phương trình trên ta thu được: