Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình xin phép sửa đề:
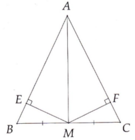
Cho tam giac ABC cân tại A, M là trung điểm của BC, ME vuông góc với AB, MF vuông góc với AC. Chứng minh ME = MF và AM là đường trung trực của EF.
\(\text {(1)}\)
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat {B}= \widehat {C}(\text {Tam giác ABC cân tại A})\)
`MB = MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`->`\(\widehat {BAM}=\widehat {CAM} (\text {2 góc tương ứng})\)
Xét Tam giác `AEM` và Tam giác `AFM` có:
`\text {AM chung}`
\(\widehat{BAM}=\widehat{CAM} (CMT)\)
\(\widehat{AEM}=\widehat{AFM} (=90^0)\)
`=> \text {Tam giác AEM = Tam giác AFM (ch-gn)}`
`-> ME = MF (2 cạnh tương ứng)`
\(\left(2\right)\)
Gọi `I` là giao điểm của `AM` và `EF`
C1:
Vì Tam giác `AEM =` Tam giác `AFM (\text {Theo CMT})`
`-> AE = AF (\text {2 cạnh tương ứng})`
Xét Tam giác `AEI` và Tam giác `AFI` có:
`AE = AF (CMT)`
\(\widehat{EAI}=\widehat{FAI} (\text {Theo CMT})\)
`\text {AI chung}`
`=> \text {Tam giác AEI = Tam giác AFI (c-g-c)}`
`-> IE = IF (\text {2 cạnh tương ứng})`
`->`\(\widehat{AIE}=\widehat{AIF} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIE}+\widehat{AIF}=180^0\)
`->`\(\widehat{AIE}=\widehat{AIF}=\)`180/2=90^0`
`-> \text {AI} \bot \text {EF}`
\(\text{Ta có: }\left\{{}\begin{matrix}\text{IE = IF }\\\text{AI}\perp\text{EF}\end{matrix}\right.\)
`-> \text {AI là đường trung trực của EF}`
`-> \text {AM là đường trung trực của EF}`
C2 (nếu bạn đã học về tính chất của tam giác cân với các đường Trung Tuyến, Đường Cao, Đường Trung Trực) :
Ta có:
AM vừa là đường phân giác, vừa là đường trung tuyến
`*` Theo tính chất của tam giác cân
`-> \text {AM là đường trung trực của EF (đpcm)}`
`@`\(\text{dnammv}\)
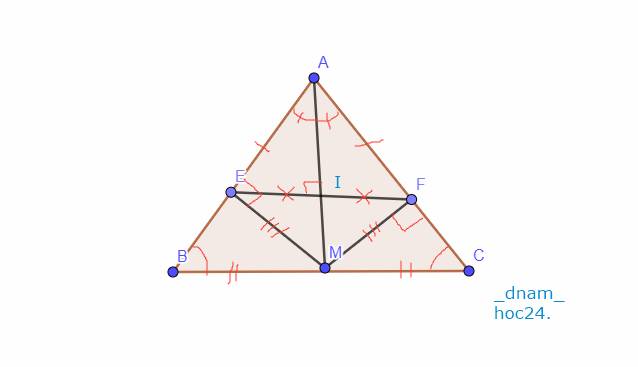

a, xét \(\Delta\)BEM và \(\Delta\)CFM có:
\(\widehat{B}\)=\(\widehat{C}\)(gt)
BM=CM(trung tuyến AM)
\(\Rightarrow\)\(\Delta\)BEM=\(\Delta\)CFM(CH-GN)
b,Ta có \(\Delta\)ABM=\(\Delta\)ACM(c.c.c)
\(\Rightarrow\)\(\widehat{BAM}\)=\(\widehat{CAM}\)
Gọi O là giao của AM và EF
xét tam giác OAE và tam giác OAF có:
AO cạnh chung
\(\widehat{OAE}\)=\(\widehat{OAF}\)(cmt)
vì AB=AC mà EB=FC nên AE=AF
\(\Rightarrow\)tam giác OAE=tam giác OAF(c.g.c)
\(\Rightarrow\)\(\widehat{AOE}\)=\(\widehat{AOF}\)mà 2 góc này ở vị trí kề bù nên\(\widehat{AOE}\)=\(\widehat{AOF}\)=90 độ(1)
\(\Rightarrow\)OE=OF suy ra O là trung điểm EF(2)
từ (1) và (2) suy ra AM là đg trung trực của EF
c, vì \(\widehat{BAM}\)=\(\widehat{CAM}\)=> AM là p/g của \(\widehat{BAC}\)(1)
ta có tam giác BAM=tam giác CAM(c.g.c)
=> AD là p/g của góc BAC(2)
từ (1) và(2) suy ra AM và AD trùng nhau nên A,M,D thẳng hàng
a, Ta có : Tam giác ABC cân tại A => Góc B=Góc C
Xét tam giác BEM vuông tại E và tam giác CFM vuông tại F
BM=CM (BM là trung tuyến)
Góc B=Góc C
=> Tam giác BEM=Tam giác CFM(ch-gn)
b,Từ a, \(\Delta\)BEM=\(\Delta CFM\)=> ME=MF (1);BE=FC
Mà AB=AC=> AE=AF(2)
Từ 1 và 2 => AM là trung trực của EF

a/ Xét tam giác BEM và tam giác CFM có:
Góc B=C(Tam giác ABC cân tại A)
Góc BEM=CFM(Tam giác ABC cân tại A)
BM=MC(Trung tuyến AM)
=> Tam giác BEM=tam giác CFM(ch-gn)
b/Gọi giao điểm của EF và AM là O.
Vì AM là trung tuyến của tam giác cân nên AM cũng là đường cao của tam giác cân ABC.
=> Góc AMB=AMC=90 độ.
Mà Góc EMB=FMC(góc tương ứng của tam giác EMB=tam giác FMC)
=> Góc EMO=FMO.
Xét tam giác EMO và tam giác FMO có:
EM=MF(cạnh tương ứng trong tam giác EMB= tam giác FMC)
Góc EMO=FMO(cmt)
MO chung
=> Tam giác EMO=tam giác FMO(c-g-c)
=> Góc EOM=FOM(góc tương ứng)=180 độ/2=90 độ
EO=OF(cạnh tương ứng)
=> AM là đường trung trực của EF.
c/ Vì AI=\(\frac{8}{3}\)cm nên AM có độ dài là: \(\frac{8}{3}:\frac{2}{3}=4\)cm(tính chất trọng tâm tam giác)
Áp dụng định lí Pytago vào tam giác vuông AMC, ta được:
AC2=AM2+MC2=42+MC2=52=25
=> MC=\(\sqrt{\left(5^2-4^2\right)}=3\)cm
Mà BM=MC(Trung tuyến AM)
=> BC=3+3=6cm

A B C M E F
a/ Ta có :
\(\Delta ABC\) cân tại A
Lại có : AM là đường trung tuyến ứng với BC
\(\Leftrightarrow AM\) là đường trung trực của BC (đpcm)
b/ \(\Delta BEM=\Delta CFM\left(ch-gn\right)\)
\(\Leftrightarrow ME=MF\) (đpcm)
Ta có : +) \(AB=AE+EB\) (E nằm ~ A và B)
\(AC=AF+FC\) (F nằm giữa A và C)
Mà AB = AC; EB = EC do \(\Delta BEM=\Delta CFM\)
\(\Leftrightarrow AE=À\)F
Lại có : ME = MF
\(\Leftrightarrow AM\) là đường trung trực của EF
a) \(\Delta ABC\) cân tại A mà AM là trung tuyến của BC
=> AM là trung trực của BC ( tính chất tam giác cân )
b) \(\Delta ABC\) cân tại A mà AM là trung trực của BC
=> AM là phân giác của góc A
Xét tam giác EAM và tam giác FAM
\(\widehat{AEM}=\widehat{ÀFM}=90^0\)
AM chung
\(\widehat{FAM}=\widehat{EAM}\) (AM là phân giác của góc A)
=> \(\Delta\) vuông EAM =\(\Delta\) vuông FAM ( cạnh huyền -góc nhọn )
=> AE =AF ( 2 cạnh tương ứng )
=> \(\Delta AEF\) cân tại A mà AM là phân giác của góc A
=> AM là trung trực của EF ( tính chất tam giác cân )

a: Xét ΔEBM vuông tại E và ΔFCM vuông tại F có
MB=MC
góc B=góc C
=>ΔEBM=ΔFCM
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
d: Xet ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
=>ΔABD=ΔACD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,M,D thẳng hàng