Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là đường chân cao hạ từ O đến MN
Giả sử OH = 1 → OM \(=\sqrt[4]{10};ON=\sqrt{10}\)
Do đó tính \(\widehat{MON}\approx1270,35^o\)
A đúng

\(L_A=10lg\left(\frac{I_A}{I_0}\right)\Rightarrow I_A=0,1\left(Wm^2\right)\)

Đáp án B
Mức cường độ âm tại A,B bằng nhau nên OA = OB . Mức cường độ âm tại C cực đại nên C là trung điểm của AB


Đáp án B
Vì mức cường độ âm tại A và B bằng nhau nên suy ra OA = OB. C có mức cđ âm max nên C gần O nhất, hay OC vuông góc với AB.
Có P 4 π O A 2 = I 0 .10 L P 4 π O C 2 = I 0 .10 L m ax ⇒ 10 L max − L = O A O C 2 ⇒ 10 0 , 3 = O A O C 2 ⇒ O C = 2 , 1238 ( m )
⇒ A B = 2 A C = 2 O A 2 − O C 2 ≈ 4 , 2376 ( m ) ⇒ t = A B v = 3 , 5313 ( s )
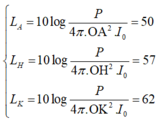
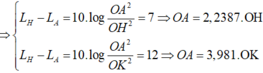
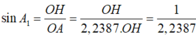
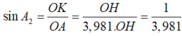
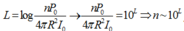

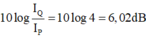
Đáp án B
Ta có mức cường độ âm:
L = 10 . log I I 0 = 10 log P 4 πR 2 . I 0 ⇒ L max ⇔ R min
(với R là khoảng cách từ nguồn âm đến điểm khảo sát)
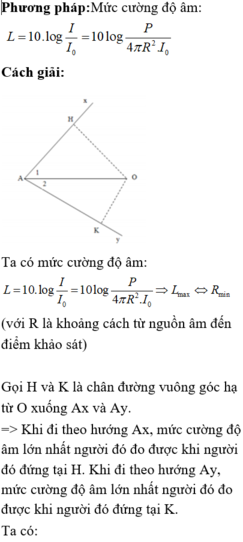
Gọi H và K là chân đường vuông góc hạ từ O xuống Ax và Ay.
=> Khi đi theo hướng Ax, mức cường độ âm lớn nhất người đó đo được khi người đó đứng tại H. Khi đi theo hướng Ay, mức cường độ âm lớn nhất người đó đo được khi người đó đứng tại K.
Ta có : L A = 10 log P 4 π . OA 2 . I 0 = 50 L H = 10 log P 4 π . OH 2 . I 0 = 57 L K = 10 log P 4 π . OK 2 . I 0 = 62
⇒ L H - L A = 10 . log OA 2 OH 2 = 7 ⇒ OA = 2 , 2387 OH L K - L A = 10 . log OA 2 OK 2 = 12 ⇒ OA = 3 , 981 OK
sin A 1 = O H O A = O H 2 , 2387 O H = 1 2 , 2387 ⇒ A 1 ^ = 26 , 53 0
sin A 2 = O K O A = O K 3 , 981 O K = 1 3 , 981 ⇒ A 2 ^ = 14 , 55 0
⇒ xAy ^ = A 1 ^ + A 2 ^ = 41 0