Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S A B C M
\(CM=\sqrt{BM^2+BC^2}=\sqrt{\left(\frac{AB}{2}\right)^2+BC^2}=\frac{a\sqrt{21}}{2}\)
Từ A kẻ \(AH\perp CM\Rightarrow\Delta AHM\sim\Delta CBM\)
\(\Rightarrow\frac{AH}{AM}=\frac{BC}{CM}\Rightarrow AH=\frac{AM.BC}{CM}=\frac{AB.BC}{2CM}=\frac{a\sqrt{42}}{7}\)
Từ A kẻ \(AK\perp SH\Rightarrow AK\perp\left(SMC\right)\Rightarrow AK=d\left(A;\left(SMC\right)\right)\)
\(\frac{1}{AK^2}=\frac{1}{AH^2}+\frac{1}{SA^2}\Rightarrow AK=\frac{AH.SA}{\sqrt{AH^2+SA^2}}=\frac{2a\sqrt{51}}{17}\)

Đáy ABCD là hình gì cạnh a bạn? Hình vuông hay hình thoi?

S A B C D H M N K
Kẻ \(AH\perp BD\Rightarrow BD\perp\left(SAH\right)\Rightarrow\widehat{SHA}\) là góc giữa (SBD) và (ABCD)
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AB^2}\Rightarrow AH=\frac{AB.AD}{\sqrt{AB^2+AD^2}}=\frac{a\sqrt{3}}{2}\)
\(SA=\sqrt{SD^2-AD^2}=2a\)
\(tan\widehat{SHA}=\frac{SA}{AH}=\frac{4\sqrt{3}}{3}\Rightarrow\widehat{SHA}\simeq66^035'\)
b/ \(MS=MA\Rightarrow d\left(S;\left(MND\right)\right)=d\left(A;\left(MND\right)\right)\)
Từ A kẻ \(AK\perp MD\Rightarrow AK\perp\left(MND\right)\Rightarrow AK=d\left(A;\left(MND\right)\right)\)
\(AM=\frac{SA}{2}=a\Rightarrow\frac{1}{AK^2}=\frac{1}{AM^2}+\frac{1}{AD^2}\Rightarrow AK=\frac{AM.AD}{\sqrt{AM^2+AD^2}}=\frac{a\sqrt{3}}{2}\)

Bạn tự vẽ hình
Gọi N là trung điểm BC \(\Rightarrow AN=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều ABC cạnh a)
\(SN=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều SBC cạnh a)
\(\Rightarrow AN=SN=SA=\frac{a\sqrt{3}}{2}\Rightarrow\Delta SAN\) đều
\(\left\{{}\begin{matrix}BC\perp SN\\BC\perp AN\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAN\right)\)
\(\left(P\right)\perp BC\Rightarrow\left(P\right)//\left(SAN\right)\)
Từ M kẻ \(MD//AN\left(D\in BC\right)\), từ M kẻ \(ME//SA\left(E\in SB\right)\)
\(\Rightarrow\Delta MDE\) là thiết diện của (P) và chóp
Theo đt Talet: \(\frac{MD}{AN}=\frac{ME}{SA}=\frac{DE}{SN}=\frac{BM}{AB}\)
\(\Rightarrow MD=ME=DE=\frac{AN.BM}{AB}=\frac{\frac{a\sqrt{3}}{2}\left(a-b\right)}{a}=\frac{\sqrt{3}}{2}\left(a-b\right)\)
\(\Rightarrow\Delta MDE\) là tam giác đều cạnh \(\frac{\sqrt{3}}{2}\left(a-b\right)\)
Theo công thức diện tích tam giác đều:
\(S_{MDE}=\frac{\left(\frac{\sqrt{3}}{2}\left(a-b\right)\right)^2\sqrt{3}}{4}=\frac{3\sqrt{3}}{16}\left(a-b\right)^2\)

a) Gọi q là công sai của cấp số nhân. Ta có: \(a;b=aq;c=aq^2\).
\(a^2b^2c^2\left(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}\right)=\dfrac{b^2c^2}{a}+\dfrac{a^2c^2}{b}+\dfrac{a^2b^2}{c}\)
\(=\dfrac{\left(a.q\right)^2\left(a.q^2\right)^2}{a}+\dfrac{a^2\left(aq^2\right)^2}{aq}+\dfrac{a^2\left(aq\right)^2}{aq^2}\)
\(=\dfrac{a^2q^2a^2q^4}{a}+\dfrac{a^2a^2q^4}{aq}+\dfrac{a^2a^2q^2}{aq^2}\)
\(=a^3q^6+a^3q^3+a^3\)
\(=\left(a^2q\right)^3+\left(aq\right)^3+a^3\)
\(=c^3+b^3+a^3=a^3+b^3+c^3\).
b) Gọi q là công bội của của cấp số nhân.
Ta có: \(a;b=aq;c=aq^2;d=aq^3\).
\(\left(ab+bc+cd\right)^2=\left(a.aq+aq.aq^2+aq^2.aq^3\right)^2\)
\(=\left(a^2q+a^2q^3+a^2q^5\right)^2=a^4q^2\left(1+q^2+q^4\right)^2\). (1)
\(\left(a^2+b^2+c^2\right)\left(b^2+c^2+d^2\right)\)\(=\left(a^2+a^2q^2+a^2q^4\right)\left(a^2q^2+a^2q^4+a^2q^6\right)\)
\(=a^2\left(1+q^2+q^4\right)a^2q^2\left(1+q^2+q^4\right)\)
\(=a^4q^2\left(1+q^2+q^4\right)^2\). (2)
So sánh (1) và (2) ta có điều phải chứng minh.

3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)

Bạn ghi lại đề, đề bài từ đoạn "gọi M, Q..." trở đi là thấy ko chính xác nữa
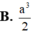
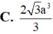
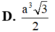
Đáp án là B
Ta có đáy là hı̀nh thoi có một góc 120 0 nên diện tı́ch đáy bằng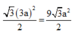
do lăng trụ đứng nên ta có thể tı́ch khối lăng trụ bằng 27 3 a 3 2