Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15



hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

đừng có hỏi các bạn ở đây bằng những câu hỏi hàng tuần ở Online Math bạn ạ,đó là gian lận đấy



TA CÓ:
= 1+\(\frac{1}{2^2}\)+\(\frac{1}{3^2}\)+.....+\(\frac{1}{49^2}\)+\(\frac{1}{50^2}\)<1+ \(\frac{1}{1\times2}\)+\(\frac{1}{2\times3}\)+....+\(\frac{1}{49\times50}\)
= 1+ 1- \(\frac{1}{2}\) + \(\frac{1}{2}\) - \(\frac{1}{3}\) + ..... + \(\frac{1}{49}\) - \(\frac{1}{50}\)
= 1+ 1 - \(\frac{1}{50}\)
= 1+ \(\frac{49}{50}\) < 2
Chứng tỏ A < 2

Để x=1 là nghiệm của f(x)
thì a.13+b.12+c.1+d=0
<=>a+b+c+d=0
Vậy..........

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)
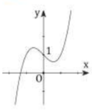
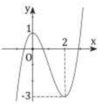
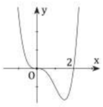
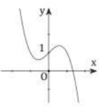
Đáp án A
Hàm số y = f x = x 3 − x + 1 là hàm đa thức bậc 3 nên loại đáp C.
Đồ thị hàm số có dạng của hàm bậc 3 với hệ số a> 0 => Loại đáp án D.
Đồ thị hàm số không có cực trị tại x = 0 nên loại B.