Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Electron chuyển động đều tức là lực điện cân bằng với lực từ:
\(F_E=F_B\)
\(\Rightarrow eE=evB\)
\(\Rightarrow v=\frac{E}{B}=10^6\left(\text{m/s}\right)\)
Động năng của electron:
\(T=\frac{m_ev^2}{2}\)
Năng lượng của photon cung cấp công thoát cho electron và cho electron vận tốc đầu (động năng):
\(h\frac{c}{\lambda}\text{=}E_{th}+T\) (\(E_{th}\)là công thoát)
\(\lambda=\frac{hc}{E_{th}+T}=1,7.10^{-7}\left(m\right)=0,17\left(nm\right)\)
\(chọn.A\)

Câu trả lời ở đây bạn nhé
Câu hỏi của lý - Học và thi online với HOC24

Đáp án: D
+ Do e không bị lệch hướng nên e.E = B.ev
=> v = 5.106 m/s.
+ Từ đó ta tính được:
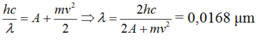

câu hỏi của bn có ở đây nhá Câu hỏi của HOC24 - Học và thi online với HOC24

Đáp án: B
Sử dụng phương trình Anhxtanh ta được:
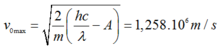
Khi chuyển động trong điện trường đều và từ trường hướng vuông góc với nhau, e chuyển động thẳng đều khi lực điện cân bằng với lực lorenxo khi đó ta có:
e.vmaxB = e.E
→E = 1258V/m

Đáp án: D
Áp dụng định lý biến thiên động năng ta có:
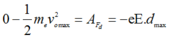
(vì lực điện trường tác dụng lên e có chiều ngược với chiều điện trường)
dmax là quãng đường tối đa mà vật đi được trong điện trường.
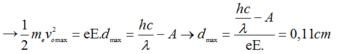

Số lượng photon đến bản A bằng năng lượng của chùm photon chia cho năng lượng mỗi photon
\(N=\frac{Pt}{\varepsilon}\)
Số lượng electron bật ra là
\(N'=N.H=0,01N\)
Số electron đến bản B là
\(N''=\frac{q}{e}=\frac{It}{e}\)
Tỉ lệ số photon rời A đến được B là
\(\frac{N''}{N'}=\frac{I\varepsilon}{eHP}\approx0,218\)
Phần trăm rời A mà không đến B là
\(\text{1-0.218=0.782=78.2%}\)
Chọn đáp án C
@ Lời giải:
+ Vận tốc cực đại ban đầu của electron quang điện: v = 2 m e h c λ − A (chú ý đơn vị: tính vận tốc thì A, ε phải đổi đơn vị J)
+ Thay số vào ta được: v = 402721m/s
+ Để các electron vẫn tiếp tục chuyển động thẳng và đều thì cường độ điện trường E → thì lực điện và lực lorenxo phải cân bằng nhau. Khi đó:
qE = qvB → E = vB → B = 201,36 (V/m)
+ Chú ý: Bài này ta không cần quan tâm đến phương, chiều của lực điện và lực lorenxo. Chỉ cần điều kiện cho hai lực này cân bằng nhau là đủ.