Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.

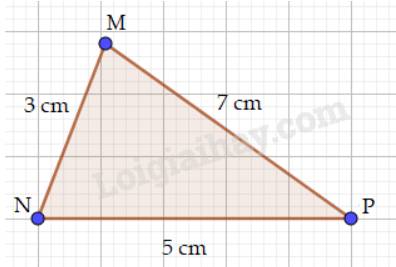
Góc P đối diện với cạnh MN
Góc M đối diện với cạnh NP
Góc N đối diện với cạnh MP.
Ta có: MN < NP < MP nên \(\widehat P < \widehat M < \widehat N\)( định lí)
Vậy sắp xếp các góc của tam giác MNP theo thứ tự từ bé đến lớn là: \(\widehat P;\widehat M;\widehat N\).

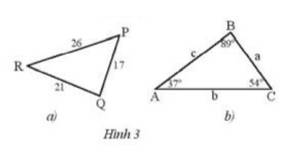
a) Ta có độ dài các cạnh tam giác PQR theo thứ tự từ nhỏ đến lớn là PQ, QR, RP
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ra có các góc tam giác PQR theo thứ tự từ nhỏ đến lớn là R, P, Q
b) Ta có số đo các góc theo tứ tự từ nhỏ đến lớn của tam giác ABC là A, C, B
Vì trong tam giác góc đối diện cạnh lớn hơn thì lớn hơn
Nên ta có các cạnh tam giác ABC theo thứ tự từ nhỏ đến lớn là a, c, b.

A B C D E H K
Trên AB lấy điểm H sao cho ^ACH=600. Gọi CH giao AD tại điểm K. Nối K với E.
Xét \(\Delta\)ACD và \(\Delta\)CAH có:
^ACD=^CAH=800
Cạnh AC chung => \(\Delta\)ACD=\(\Delta\)CAH (g.c.g)
^CAD=^ACH=600
=> AD=CH (2 cạnh tương ứng). Mà \(\Delta\)AKC đều theo cách vẽ => AC=CK=AK và ^ACK=^CAK=^AKC=600
Ta có: ^AKC=^HKD => ^HKD=600 (1)
AD=CH => AK+KD=CK+KH (2). Thay AK=CK vào (2) => KD=KH (3)
Từ (1) và (3) => \(\Delta\)HKD đều => KD=HD=KH và ^HKD=^KHD=^KDH=600
Xét \(\Delta\)CAE: ^AEC=1800 - (^CAE+^ACE) = 1800-(800+500)=1800-1300=500
=> ^AEC=^ACE=500 => \(\Delta\)CAE cân tại A => AC=AE. Mà AC=AK (cmt)
=> AE=AK => \(\Delta\)EAK cân tại A.
Ta có: ^EAK=^BAC-^CAK=800-600=200 => ^AKE=^AEK=(1800-200)/2 = 1600/2=800
Lại có: ^EKH=180-(^AKE+^HKD)=1800-(800+600)=1800-1400=400 => ^EKH=400 (4)
Xét \(\Delta\)CAH: ^AHC=1800-(^ACH+^CAH)=1800-(600+800)=1800-1400=400 => ^AHC=400 hay ^EHK=400 (5)
Từ (4) và (5) => \(\Delta\)KEH cân tại E => EK=EH.
Xét \(\Delta\)EKD và \(\Delta\)EHD có:
KD=HD (cmt)
Cạnh ED chung => \(\Delta\)EKD=\(\Delta\)EHD (c.c.c) => ^KDE=^HDE (2 góc tương ứng)
EK=EH (cmt)
=> ^KDE=^HDE=^KDH/2. Mà ^KDH=600 (cmt) => ^KDE=^HDE=600/2=300
=> ^KDE=300 hay ^ADE=300.
Vậy góc ADE=300.

Áp dụng định lí tổng ba góc trong một tam giác trong tam giác MNP, có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = 180^\circ \\ \Rightarrow 47^\circ + 53^\circ + \widehat P = 180^\circ \\ \Rightarrow \widehat P = 180^\circ - 47^\circ - 53^\circ = 80^\circ \\ \Rightarrow \widehat M < \widehat N < \widehat P(47^\circ < 53^\circ < 80^\circ )\end{array}\)
\( \Rightarrow \) NP < MP < MN ( cạnh đối diện với góc lớn hơn thì lớn hơn)
Vậy các cạnh của tam giác đó theo thứ tự độ dài từ bé đến lớn là NP, MP, MN.

Sắp xếp các gốc theo thứ tự từ lớn đến bé:
Ta có: \(AC>BC>AB\)
\(\Rightarrow\widehat{B}>\widehat{A}>\widehat{C}\)
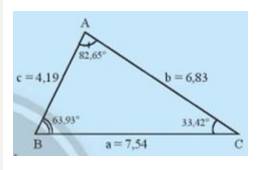
- AB < AC < BC nên sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn là: AB, AC, BC.
\(\widehat C < \widehat B < \widehat A\) nên sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn là: \(\widehat C;\widehat B;\widehat A\)
- Góc lớn nhất là góc A đối diện với cạnh BC. Góc bé nhất là góc C đối diện với cạnh AB.