K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 11 2021
\(a,=\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}=-\sqrt{a}\\ b,=\dfrac{\sqrt{p}\left(\sqrt{p}-2\right)}{\sqrt{p}-2}=\sqrt{p}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 9 2021
ĐKXĐ: \(x\ge0;x\ne4\)
\(A=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{3\sqrt{x}-6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+2\right)}-\dfrac{12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
9 tháng 9 2021
\(C=\left(\dfrac{3}{x-1}+\dfrac{1}{\sqrt{x}+1}\right):\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{3+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)
HA
7 tháng 9 2015
\(\frac{a\left(a-1\right)}{a-1}-\frac{a\left(-6a+5\right)}{a-1}=\frac{a^2-a+6a^2-5a}{a-1}\)
=\(\frac{7a^2-6a}{a-1}\)
19 tháng 7 2021
a) Ta có: \(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\)
\(=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b) Để B=16 thì \(4\sqrt{x+1}=16\)
\(\Leftrightarrow x+1=16\)
hay x=15
DN
7 tháng 5 2017
Trước hết ta sẽ giải quyết phần \(\sqrt{5-2\sqrt{3-\sqrt{3}}}\)
ta có công thức rút gọn sau: \(S+_-2\sqrt{P}\Rightarrow x^2-Sx+P\Leftrightarrow x_1=a;x_2=b\Rightarrow S+2\sqrt{P}=\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(\sqrt{5-2\sqrt{3-\sqrt{3}}}\Rightarrow x^2-5x+3\sqrt{3}=0\left(1\right)\)
\(\left(a=1;b=-5;c=3-\sqrt{3}\right)\)
\(\Delta=b^2-4ac=\left(-5\right)^2-4.1.\left(3-\sqrt{3}\right)=13+4\sqrt{3}>0\)
\(\sqrt{\Delta}=\sqrt{13+4\sqrt{3}}=\sqrt{\left(2\sqrt{3}+1\right)^2}=2\sqrt{3}+1\)
Phương trình (1) có 2 nghiệm phân biệt:
\(x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-\left(-5\right)+2\sqrt{3}+1}{2.1}=3+\sqrt{3}\)
\(x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-\left(-5\right)-\left(2\sqrt{3}-1\right)}{2.1}=2-\sqrt{3}\)
\(\Rightarrow\sqrt{5-2\sqrt{3-\sqrt{3}}}=\sqrt{\left(\sqrt{3+\sqrt{3}}-\sqrt{2-\sqrt{3}}\right)^2}=\sqrt{3+\sqrt{3}}-\sqrt{2-\sqrt{3}}\)
\(F=\sqrt{3+\sqrt{3}}-\sqrt{2-\sqrt{3}}-\sqrt{3+\sqrt{3}}+\sqrt{2+\sqrt{3}}\)
\(\Leftrightarrow F=\sqrt{2+\sqrt{3}}-\sqrt{2-\sqrt{3}}\)
Nhân cả tử và mẫu của hai căn với căn 2
Từ đó ta sẽ được hằng đẳng thức ở tử và rút gọn mất căn:
\(\Leftrightarrow F=\frac{\sqrt{3}+1}{\sqrt{2}}-\frac{\sqrt{3}-1}{\sqrt{2}}=\sqrt{2}\)
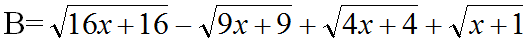
ĐKXĐ: \(x>2\)
\(A=\dfrac{\sqrt{x-2-4\sqrt{x-2}+4}+\sqrt{x-2+4\sqrt{x-2}+4}}{\sqrt{\left(\dfrac{2}{x}-1\right)^2}}\)
\(=\dfrac{\sqrt{\left(\sqrt{x-2}-2\right)^2}+\sqrt{\left(\sqrt{x-2}+2\right)^2}}{\left|\dfrac{2}{x}-1\right|}=\dfrac{\left|\sqrt{x-2}-2\right|+\left|\sqrt{x+2}+2\right|}{1-\dfrac{2}{x}}\)
- Với \(x\ge6\Rightarrow A=\dfrac{\sqrt{x-2}-2+\sqrt{x-2}+2}{\dfrac{x-2}{x}}=\dfrac{2x\sqrt{x-2}}{x-2}=\dfrac{2x}{\sqrt{x-2}}\)
- Với \(2< x< 6\Rightarrow A=\dfrac{2-\sqrt{x-2}+\sqrt{x-2}+2}{\dfrac{x-2}{x}}=\dfrac{4x}{x-2}\)
em cảm ơn ạ