Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(27y^3-9y^2+y-\dfrac{1}{27}\)
\(=\left(3y-\dfrac{1}{3}\right)^3\)

a: \(x^3-2x+4\)
\(=x^3+2x^2-2x^2-4x+2x+4\)
\(=\left(x+2\right)\left(x^2-2x+2\right)\)
b: \(x^3-4x^2+12x-27\)
\(=\left(x-3\right)\left(x^2+3x+9\right)-4x\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-x+9\right)\)
c: \(x^3+2x^2+2x+1\)
\(=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+1\right)\)

\(9x^6-12x^7+4x^8\)
\(=x^6\left(4x^2-12x+9\right)\)
\(=x^6.\left(2x-3\right)^2\)
hk
tốt

\(\left(x-2\right)^3-1=\left(x-2\right)\left[\left(x-3\right)^2+x-2\right]=\left(x-2\right)\left(x^2+5x+7\right)\)
\(\left(x+3y\right)^2-9y^2=x\left(x+6y\right)\)
\(\left(x+3\right)^2-\left(x-1\right)^2=4\left(2x+4\right)=8\left(x+2\right)\)
a) \(\left(x-2\right)^3-1=\left(x-2\right)^3-1^3=\left(x-2-1\right)\left[\left(x-2\right)^2+\left(x-2\right)\cdot1+1^2\right]\)\(=\left(x-3\right)\left(x^2-4x+4+x-2+1\right)\)
\(=\left(x-3\right)\left(x^2-3x+3\right)\)
b) \(\left(x+3y\right)^2-9y^2\)
\(=\left(x+3y\right)^2-\left(3y\right)^2\)
\(=\left(x+3y+3y\right)\left(x+3y-3y\right)\)
\(=x\left(x+6y\right)\)
c) \(\left(x+3\right)^2-\left(x-1\right)^2\)
\(=\left(x+3-x+1\right)\left(x+3+x-1\right)\)
\(=4\left(2x+2\right)\)
\(=8\left(x+1\right)\)

\(x^4-x^2+2x-1\)
\(=x^4-\left(x^2-2x+1\right)\)
\(=x^4-\left(x-1\right)^2\)
\(=\left(x^2-x+1\right)\left(x^2+x-1\right)\)
hk
tốt

Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)

a) \(-x^3+9x^2-27x+27=-\left(x^3-3.3.x^2+3.3^2.x-3^3\right)=-\left(x-3\right)^3\)
b)\(x^4-2x^3-x^2+2x+1=x^4+\left(-x\right)^2+\left(-1\right)^2+2x^2\left(-x\right)+2.\left(-x\right).\left(-1\right)+2x^2.\left(-1\right)\)
\(=\left(x^2-x-1\right)^2\)
c)\(8x^3+27y^3+36x^2y+54xy^2=\left(2x\right)^3+3.\left(2x\right)^2.3y+3.2x.\left(3y\right)^2+\left(3y\right)^3\)
\(=\left(2x+3y\right)^2\)
Phân tích thành nhân tử : -4x^2+12xy-9y^2+25(sử dụng hằng đẳng thức)
giúp mink với, mink đang cần gấp

\(=-2x^2+6xy-3y^2+25\)
\(=-\left(2x^2-6xy+3y^2\right)+25\)
\(=-\left(2x^2+3y^2\right)+25\)
\(=\left(2x^2-3y^2\right)+25\)
\(=\left(2x^2+3y^2\right).\left(2x^2-3y^2\right)+25\)

a) \(xy+y^2-x-y=y\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(y-1\right)\)
b) \(25-x^2+4xy-4y^2=25-\left(x-2y\right)^2=\left(5-x+2y\right)\left(5+x-2y\right)\)
c) \(x^2-4x+3=x^2-x-3x+3=x\left(x-1\right)-3\left(x-1\right)=\left(x-1\right)\left(x-3\right)\)
d) \(y^2\left(x-1\right)-7y^3+7xy^3\)
\(=y^2\left(x-1-7y+7xy\right)\)
\(=y^2\left[\left(x-1\right)-7y\left(1-x\right)\right]=y^2\left(x-1\right)\left(1+7y\right)\)
a)
\(xy+y^2-x-y\\ =\left(xy-x\right)+\left(y^2-y\right)\\ =x\left(y-1\right)+y\left(y-1\right)\\ =\left(y-1\right)\left(x+y\right)\)
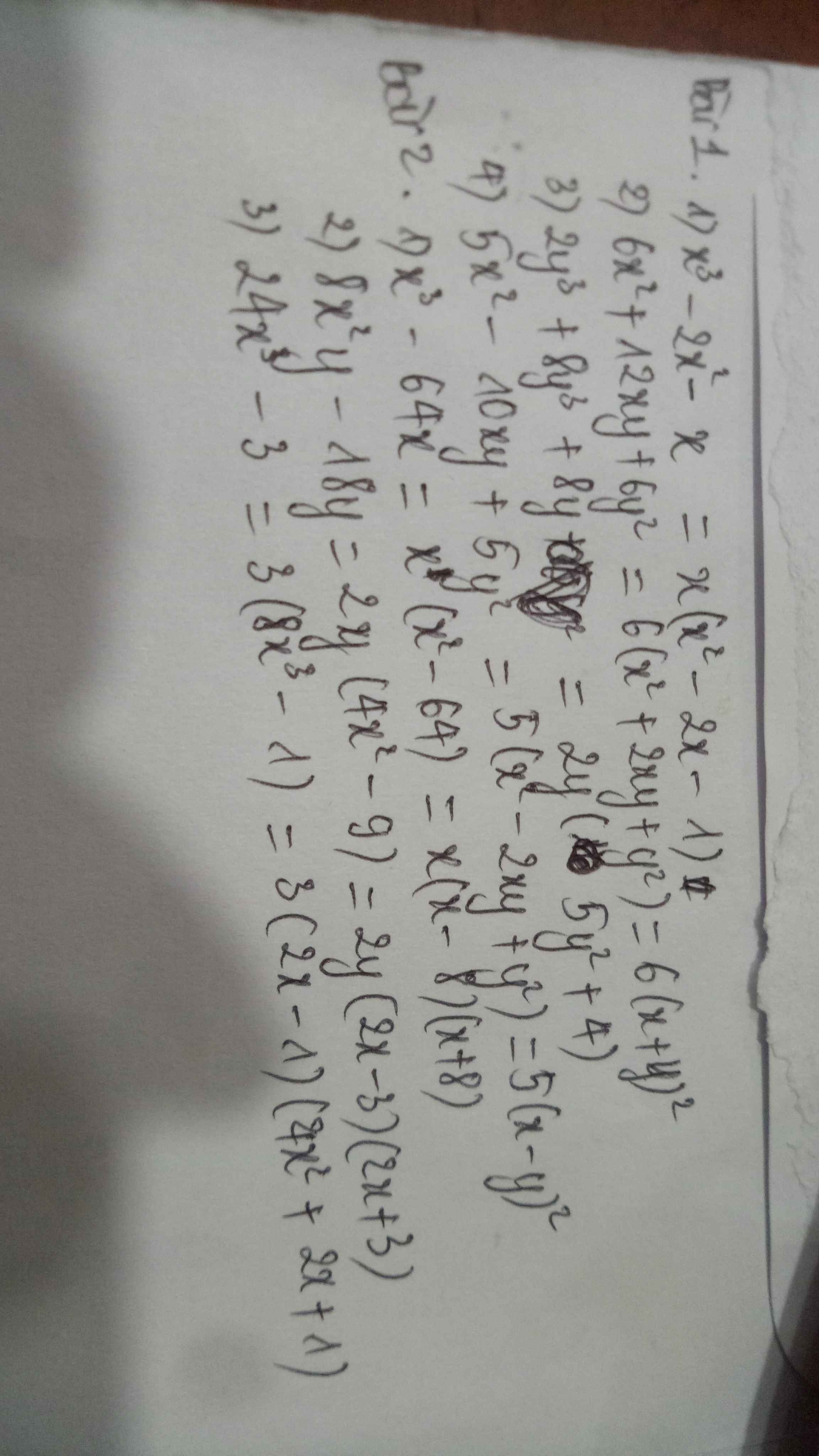
\(27y^3-9y^2+y-\frac{1}{27}\)
\(=\left(3y\right)^3-3.\left(3y\right)^2.\frac{1}{3}+3.3y.\left(\frac{1}{3}\right)^2-\left(\frac{1}{3}\right)^3\)
\(=\left(3y-\frac{1}{3}\right)^3\)
hk
tốt
7 Năm Rồi Ư!?