Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \({\left( {\frac{{17}}{{12}} - 1} \right)^2} + {\left( {2 - 1} \right)^2} = \frac{{169}}{{144}}\), nên điểm M thuộc (C)
Đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\) có tâm \(I(1;1)\)
Phương trình tiếp tuyến d của (C) tại \(M\left( {\frac{{17}}{{12}};2} \right)\) là:
\(\begin{array}{l}\left( {\frac{{17}}{{12}} - 1} \right)\left( {x - \frac{{17}}{{12}}} \right) + \left( {2 - 1} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{5}{2}x + y - \frac{{133}}{{24}} = 0\end{array}\)

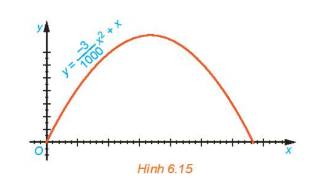
a) Tung độ đỉnh của hàm số \(y = \frac{{ - 3}}{{1000}}{x^2} + x\) là:
\(\frac{{ - \Delta }}{{4a}} = \frac{{ - \left( {{1^2} - 4.\frac{{ - 3}}{{1000}}.0} \right)}}{{4.\frac{{ - 3}}{{1000}}}} = \frac{{250}}{3}\)
Vậy độ cao cực đại của vật là \(\frac{{250}}{3}(m)\)
b) Vật chạm đất khi:
\(y = 0 \Leftrightarrow \frac{{ - 3}}{{1000}}{x^2} + x = 0 \Leftrightarrow x = \frac{{1000}}{3}\)và x=0(loại)
Vậy khoảng cách từ điểm chạm mặt đất sau khi bay của vật đến gốc O là \(\frac{{1000}}{3}\left( m \right)\)

Khi tới vị trị M(3;4), vật bị văng khỏi quỹ đạo tròn và ngay sau đó bay theo hướng tiếp tuyến d của đường tròn tại điểm M. Do đó, d đi qua điểm M và nhận vecto \(\overrightarrow {OM} = \left( {3;4} \right)\) làm vecto pháp tuyến. Vậy phương trình của d là: \(3\left( {x - 3} \right) + 4\left( {y - 4} \right) = 0 \Leftrightarrow 3x + 4y - 25 = 0\).

Người đó chuyển động theo quỹ đạo đường tròn nên để xác định phương trình quỹ đạo chuyển động của người đó ta cần phải lập phương trình đường tròn.

Để xác định điểm M ta cần giải hệ phương trình gồm hai phương trình đường thẳng của hai đường thẳng a và b

a) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 7 \Leftrightarrow - 4,9{t^2} + 10t - 5,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 5,4\) có \(\Delta = - \frac{{146}}{{25}} < 0\) và \(a = - 4,9 < 0\)
nên \(f\left( x \right)\) âm với mọi t, suy ra bât phương trình \( - 4,9{t^2} + 10t + 1,6 > 7\) vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 5 \Leftrightarrow - 4,9{t^2} + 10t - 3,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 3,4\) có hai nghiệm phân biệt là \({t_1} \simeq 0,43;{t_2} \simeq 1,61\) và \(a = - 4,9 < 0\)
nên \(f\left( t \right)\) dương khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)
Vậy khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)giây thì bóng ở độ cao trên 5 m

a) Phương trình tham số của đường thẳng \(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\)
b) Thay \(t = 2\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.2 = 81\\y = 1 + 30.2 = 61\end{array} \right.\)
Vậy khi \(t = 2\) thì tọa độ của ô tô là \(\left( {81;61} \right)\)
Thay \(t = 4\) vào phương trình\(d:\left\{ \begin{array}{l}x = 1 + 40t\\y = 1 + 30t\end{array} \right.\) ta được \(\left\{ \begin{array}{l}x = 1 + 40.4 = 161\\y = 1 + 30.4 = 121\end{array} \right.\)
Vậy khi \(t = 4\) thì tọa độ của ô tô là \(\left( {161;121} \right)\)

Trong toán học, mỗi cách chọn 2 vận động viên từ 8 vận động viên để tạo thành một cặp đấu được gọi là một tổ hợp chập 2 của 8.

Để xác định tọa độ của máy bay trực thăng ta sử dụng biểu thức tọa độ của 2 vectơ
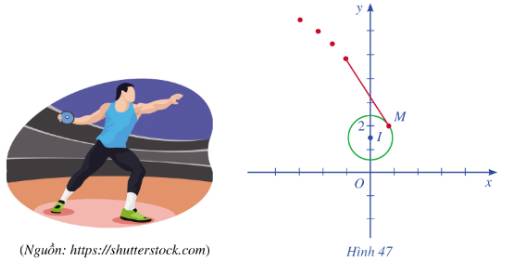




Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\begin{array}{l}\left( {\frac{{\sqrt {39} }}{{10}} - 0} \right)\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 - \frac{3}{2}} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{{\sqrt {39} }}{{10}}\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \frac{1}{2}\left( {y - 2} \right) = 0\\ \Leftrightarrow \sqrt {39} x + 5y - 13,9 = 0\end{array}\)
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\left(\dfrac{\sqrt{39}}{10}-0\right)\left(x-\dfrac{\sqrt{39}}{10}\right)+\left(2-\dfrac{3}{2}\right)\left(y-2\right)=0\\ \Leftrightarrow\dfrac{\sqrt{39}}{10}\left(x-\dfrac{\sqrt{39}}{10}\right)+\dfrac{1}{2}\left(y-2\right)=0\\ \Leftrightarrow\sqrt{39}x+5y-13,9=0\)