Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dùng công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Suy ra hệ:
\(A^2=3^2+\dfrac{(8\pi)^2}{\omega^2}\)
\(A^2=4^2+\dfrac{(6\pi)^2}{\omega^2}\)
Từ đó tìm được:
\(A=5cm\)
\(\omega=2\pi(rad/s)\)
Ban đầu, vật qua VTCB theo chiều âm, suy ra \(\varphi=\dfrac{\pi}{2}(rad)\)
Vậy PT dao động: \(x=5\cos(2\pi t+\dfrac{\pi}{2})cm\)
Chọn A
+ Thay (x1 = 3cm; v1 = 8π cm/s) và (x2 = 4cm; v2 = 6π cm/s) vào 
ta được hệ phương trình hai ẩn A2 và 
. Giải hệ phương trình ta được A = 5cm và ω = 2π rad/s.
+ Tìm giá trị các đại lượng thay vào:
+ t = 0: vật qua vị trí cân bằng theo chiều dương => φ = - π/2 rad.
+ Thay số: x = 5cos(2πt - π/2)(cm).
Chọn D.
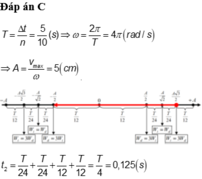
Trong thời gian 20 s thì vật thực hiện được 50 dao động toàn phần
Biên độ A = 14 : 2 = 7cm.
Gia tốc của vật đạt giá trị cực tiểu là a = \(-\omega^2A\)(khi ở biên độ dương)(bạn cần phân biệt giá trị cực tiểu với độ lớn cực tiểu).
Biểu diễn bằng véc tơ quay ta có:
O x M N 60 0 7 -7 3,5
Chất điểm qua li độ 3,5 cm theo chiều dương ứng với véc tơ quay qua N, có gia tốc cực tiểu khi véc tơ quay qua M.
Quãng đường đi được là: S \(v_{TB}= \frac{S}{t}=\frac{31,5}{\frac{7}{6}}=27\)= 3,5 + 4.7 = 31,5 cm (do qua M 2 lần)
Thời gian: t = \(\frac{60}{360}T + T = (\frac{1}{6}+1).1 = \frac{7}{6}\)s.
Tốc độ trung bình \(v_{TB} = \frac{S}{t}=\frac{31,5}{\frac{6}{7}}=27\)(cm/s)
chọn
D
Bạn ơi cho mình hỏi là vì sao d = 2A vậy ?