Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

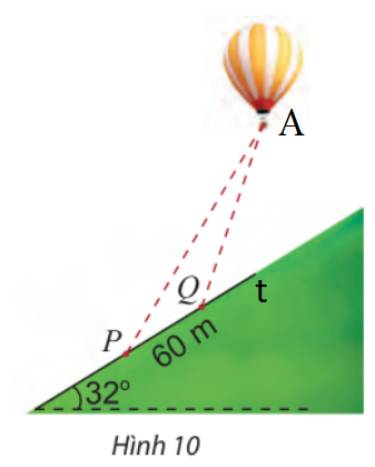
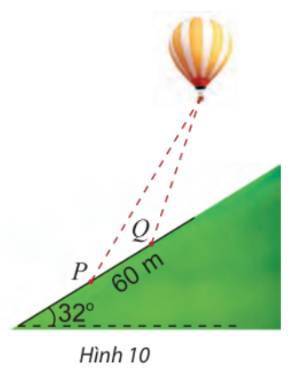
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại P, góc nâng của khinh khí cầu là \({62^ \circ }\)\( \Rightarrow \widehat P = {62^ \circ } - {32^ \circ } = {30^ \circ }\)
Tại Q, góc nâng của khinh khí cầu là \({70^ \circ }\)\( \Rightarrow \widehat {AQt} = {70^ \circ } - {32^ \circ } = {38^ \circ }\)
\( \Rightarrow \widehat {AQP} = {180^ \circ } - {38^ \circ } = {142^ \circ }\) và \(\widehat A = {180^ \circ } - {142^ \circ } - {30^ \circ } = {8^ \circ }\)
Áp dụng định lí sin trong tam giác APQ, ta có:
\(\begin{array}{l}\frac{{PQ}}{{\sin A}} = \frac{{QA}}{{\sin P}}\\ \Rightarrow QA = \sin P.\frac{{PQ}}{{\sin A}} = \sin {30^ \circ }.\frac{{60}}{{\sin {8^ \circ }}} \approx 215,56\;(m)\end{array}\)
Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.

Quãng đường vật rơi được sau t(s) là: \(h(t) = 20t + \frac{1}{2}.9,8.{t^2} = 4,9.{t^2} + 20t\)
Để vật cách mặt đất không quá 100m thì \(320 - h(t) \le 100 \Leftrightarrow h(t) \ge 220 \Leftrightarrow 4,9{t^2} + 20t - 220 \ge 0 \)
Tam thức \(f(t) = 4,9{t^2} + 20t - 220\) có \(\Delta ' = 1178 > 0\) nên f(t) có 2 nghiệm phân biệt \({t_1} = \frac {- 10 - \sqrt 1178}{4,9} ;{t_2} = \frac {- 10 + \sqrt 1178}{4,9} \) (t>0)
Mặt khác a=1>0 nên ta có bảng xét dấu:

Do t > 0 nên \(t \ge \frac {- 10 + \sqrt 1178}{4,9}\approx 5 \)
Vậy sau ít nhất khoảng 5 \(s\) thì vật đó cách mặt đất không quá 100m

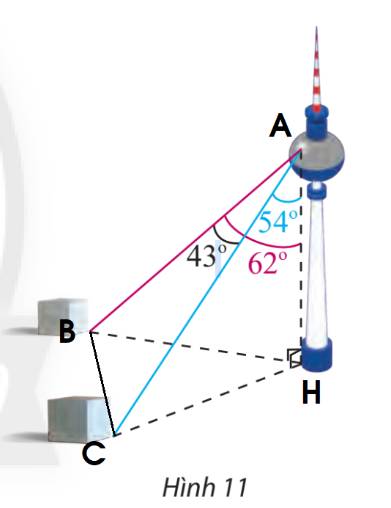
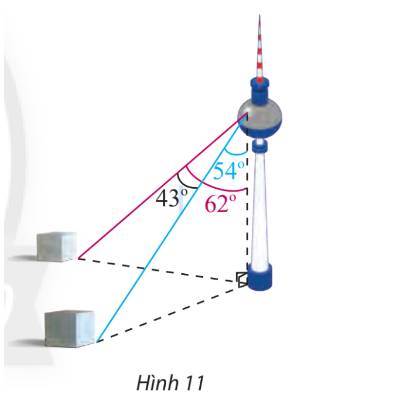
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.

Theo pt trạng thái của khí lí tưởng:
P1V1T1 =P2V2T2
⇔2.15300 = 3,5.12T2
⇒ T2 = 420 K
https://h.vn/hoi-dap/tim-kiem?q=M%E1%BB%99t+l%C6%B0%E1%BB%A3ng+kh%C3%AD+%C4%91%E1%BB%B1ng+trong+m%E1%BB%99t+xilanh+c%C3%B3+pittong+chuy%E1%BB%83n+%C4%91%E1%BB%99ng+%C4%91%C6%B0%E1%BB%A3c.+C%C3%A1c+th%C3%B4ng+s%E1%BB%91+tr%E1%BA%A1ng+th%C3%A1i+c%E1%BB%A7a+l%C6%B0%E1%BB%A3ng+kh%C3%AD+n%C3%A0y+l%C3%A0+:+2+at,+15+l%C3%ADt,+300K.+Khi+pittong+n%C3%A9n+kh%C3%AD,+%C3%A1p+su%E1%BA%A5t+c%E1%BB%A7a+kh%C3%AD+t%C4%83ng+l%C3%AAn+t%E1%BB%9Bi+3,5+at+,+th%E1%BB%83+t%C3%ADch+gi%E1%BA%A3m+c%C3%B2n+12l.+Nhi%E1%BB%87t+%C4%91%E1%BB%99+c%E1%BB%A7a+kh%C3%AD+n%C3%A9n+l%C3%A0+......&id=265613
cậu copy link tren rồi sẽ tìm ddcj loi giai như ý của tớ chưa biết viết phan số nên đừng ghi vội mà tìm theo link tren hẵng

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

- Cách 1:
Hàm số biểu diễn đồ thị \(y = - 0,00188{\left( {x - 251,5} \right)^2} + 118\)
\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)
Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)
- Cách 2:
Ta có phương trình thành cầu: \(y = – 0,00188(x – 251,5)^2 + 118\)
\( \Leftrightarrow y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai.
Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I.
Ta có: \(b = 0,94564, c = – 0,91423\)
\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I = – 0,00188(x_I – 251,5)^2 + 118 =118.\)
Vậy độ cao lớn nhất cần tìm là 118 m.



tan x=\(\frac{150}{285}\)=\(\frac{10}{19}\) ➞ x\(\approx\) 27o46'
⇒⇒ Góc hạ của tia AB là 27o46′
Gọi độ cao của khinh khí cầu là y ⇒y=285.tan 46o \(\approx\) 295 m