Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

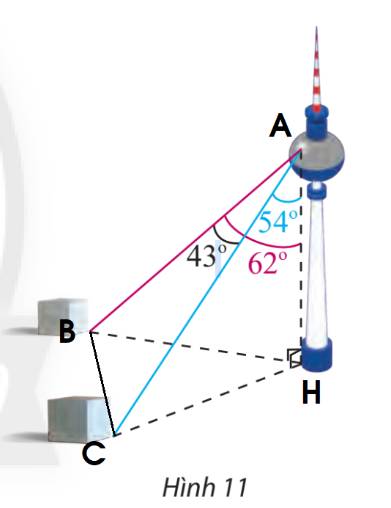
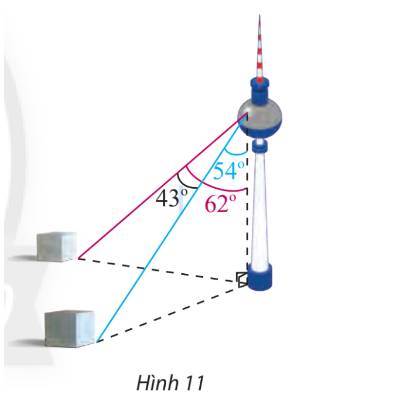
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác ABH ta có:
\(AH = 352,\;\widehat {BAH} = {62^ \circ }\)
Mà \(\cos \widehat {BAH} = \frac{{AH}}{{AB}} \Rightarrow AB = 352 : \cos {62^ \circ } \approx 749,78\)
Tương tự, ta có: \(\cos \widehat {CAH} = \frac{{AH}}{{AC}} \Rightarrow AC = 352:\cos {54^ \circ } \approx 598,86\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {749,78^2} + {598,86^2} - 2.749,78.598,86.\cos {43^ \circ }\\ \Rightarrow BC \approx 513,84\end{array}\)
Vậy khoảng cách giữa hai cột mốc này là 513,84 m.

Tam giác ABC vuông tại B nên ta có: \(\tan C = \frac{{AB}}{{CB}} \Leftrightarrow AB = \tan {32^ \circ }.(1 + x)\)
Tam giác ADB vuông tại B nên ta có: \(\tan D = \frac{{AB}}{{DB}} \Leftrightarrow AB = \tan {40^ \circ }.x\)
\(\begin{array}{l} \Rightarrow \tan {32^ \circ }.(1 + x) = \tan {40^ \circ }.x\\ \Leftrightarrow x.(\tan {40^ \circ } - \tan {32^ \circ }) = \tan {32^ \circ }\\ \Leftrightarrow x = \frac{{\tan {{32}^ \circ }}}{{\tan {{40}^ \circ } - \tan {{32}^ \circ }}}\\ \Leftrightarrow x \approx 2,9\;(km)\end{array}\)
\( \Rightarrow AB \approx \tan {40^ \circ }.2,92 \approx 2,45\;(km)\)
Vậy chiều cao của ngọn núi là 2,45 km.

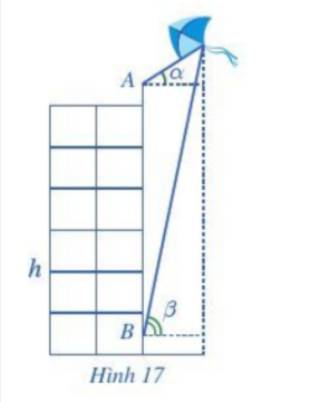
Gọi các điểm:
O là vị trí của chiếc diều.
H là hình chiếu vuông góc của chiếc diều trên mặt đất.
C, D lần lượt là hình chiếu vuông góc của A, B trên OH.
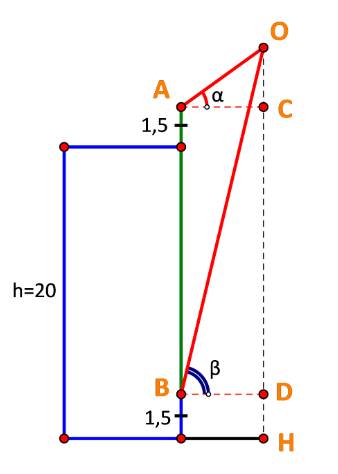
Đặt OC = x, suy ra OH = x + 20 + 1,5 =x + 21,5.
Xét tam giác OAC, ta có: \(\tan \alpha = \frac{{OC}}{{AC}} \Rightarrow AC = \frac{{OC}}{{\tan \alpha }} = \frac{x}{{\tan {{35}^o}}}\)
Xét tam giác OBD, ta có: \(\tan \beta = \frac{{OD}}{{BD}} \Rightarrow BD = \frac{{OD}}{{\tan \beta }} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
Mà:\(AC = BD\)\( \Rightarrow \frac{x}{{\tan {{35}^o}}} = \frac{{x + 20}}{{\tan {{75}^o}}}\)
\(\begin{array}{l} \Leftrightarrow x.\tan {75^o} = \left( {x + 20} \right).\tan {35^o}\\ \Leftrightarrow x = \frac{{20.\tan {{35}^o}}}{{\tan {{75}^o} - \tan {{35}^o}}} \approx 4,6\end{array}\)
Suy ra OH = 26,1.
Vậy chiếc diều bay cao 26,1 m so với mặt đất.

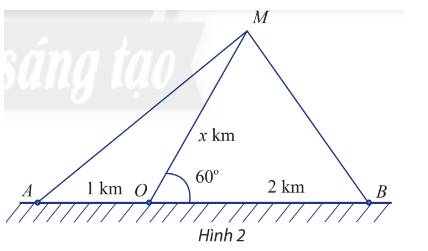
a) Đặt độ dài của MO là x km \(\left( {x > 0} \right)\)
Ta có: \(\widehat {MOA} + \widehat {MOB} = 180^\circ \) (hai góc bù nhau) \( \Rightarrow \widehat {MOA} = 120^\circ \)
Áp dụng định lý Cosin trong tam giác ta tính được:
+) Khoảng cách từ tàu đến B là \(MB = \sqrt {{x^2} + {2^2} - 2.2.x.\cos 60^\circ } = \sqrt {{x^2} - 2x + 4} \)
+) Khoảng cách từ tàu đến A là \(MA = \sqrt {{x^2} + {1^2} - 2.1.x.\cos 120^\circ } = \sqrt {{x^2} + x + 1} \)
b) Theo giải thiết ta có phương trình \(MB = \frac{4}{5}MA \Rightarrow \sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \)
\(\begin{array}{l} \Rightarrow {x^2} - 2x + 4 = \frac{{16}}{{25}}\left( {{x^2} + x + 1} \right)\\ \Rightarrow \frac{9}{{25}}{x^2} - \frac{{66}}{{25}}x + \frac{{84}}{{25}} = 0\end{array}\)
\( \Rightarrow x \simeq 1,64\) và \(x \simeq 5,69\)
Thay hai nghiệm vừa tìm được vào phương trình \(\sqrt {{x^2} - 2x + 4} = \frac{4}{5}\sqrt {{x^2} + x + 1} \) ta thấy cả hai nghiệm đều thỏa mãn phương trình
Vậy khi \(x \simeq 1,64\) hoặc \(x \simeq 5,69\) thì khoảng cách từ tàu đến B bằng \(\frac{4}{5}\) khoảng cách từ tàu đến A
c) Đổi 500 m = 0,5 km
Theo giả thiết ta có phương trình sau:
\(\begin{array}{l}MB = MO - 0,5 \Rightarrow \sqrt {{x^2} - 2x + 4} = x - 0,5\\ \Rightarrow {x^2} - 2x + 4 = {\left( {x - 0,5} \right)^2}\\ \Rightarrow {x^2} - 2x + 4 = {x^2} - x + \frac{1}{4}\\ \Rightarrow x = \frac{{15}}{4}\end{array}\)
Thay \(x = \frac{{15}}{4}\) vào phương trình \(\sqrt {{x^2} - 2x + 4} = x - 0,5\) ta thấy thỏa mãn phương trình
Vậy khi \(x = \frac{{15}}{4}\) thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500 m.

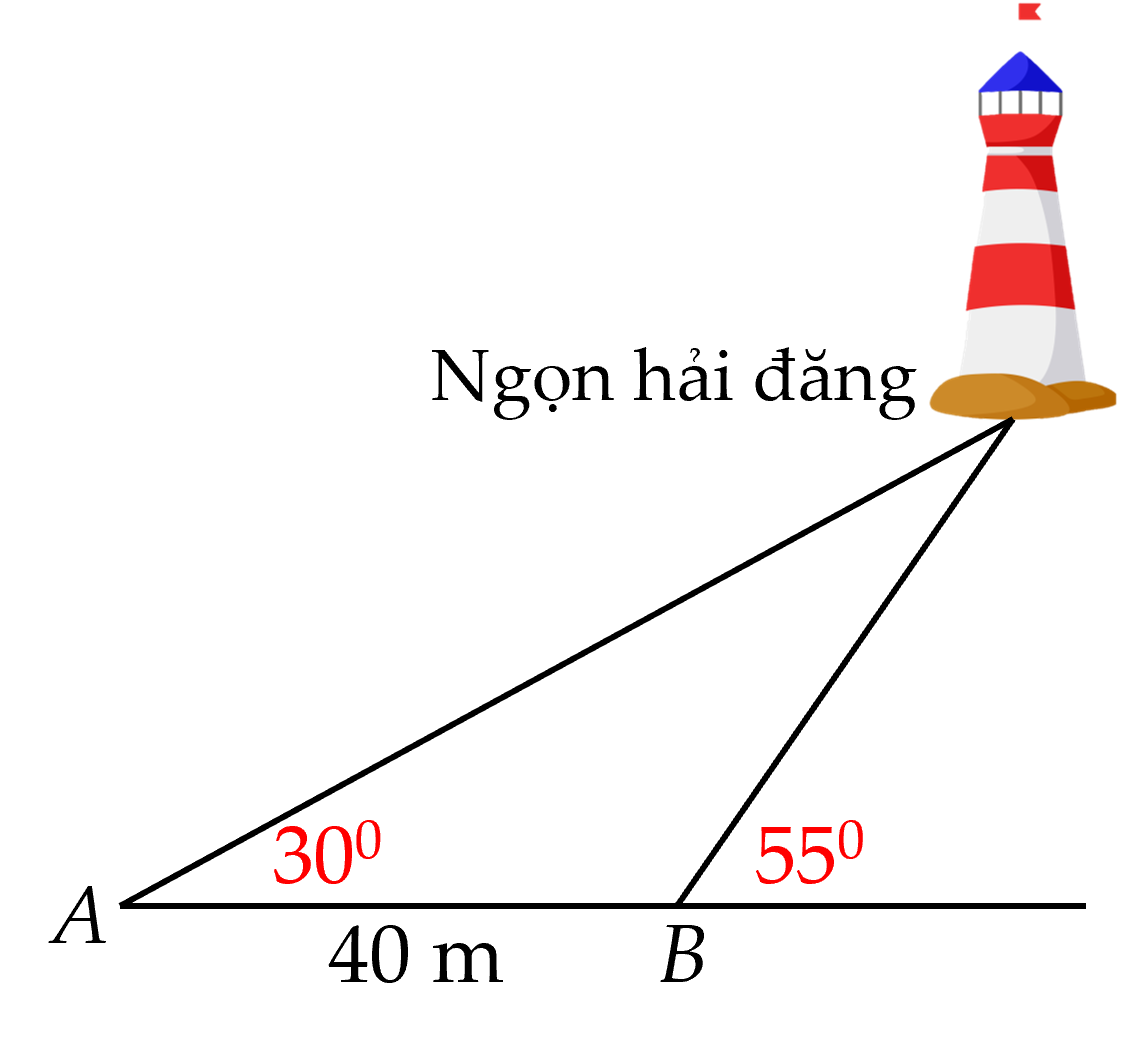
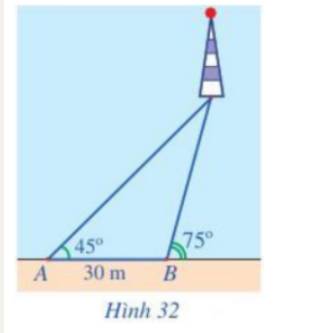
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
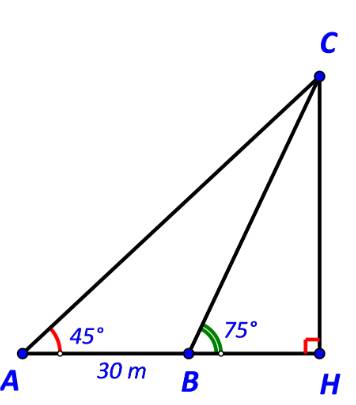
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.

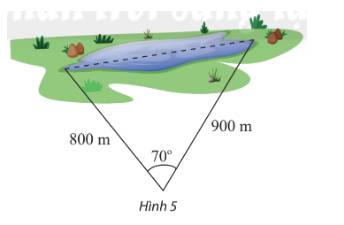
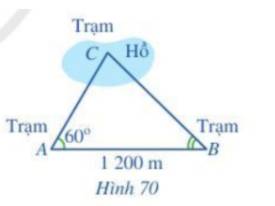
Kí hiệu hai vị trí đầu hồ và vị trí quan sát lần lượt bở các điểm A, B, C như hình dưới:
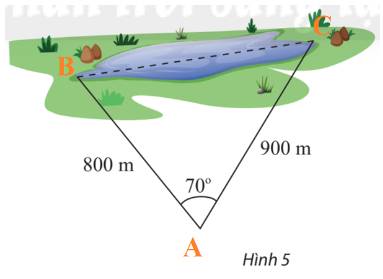
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
Mà \(AB = 800,AC = 900,\widehat A = {70^o}\)
\(\begin{array}{l} \Rightarrow B{C^2} = {900^2} + {800^2} - 2.900.800\cos {70^o} \approx 957490,9936\\ \Leftrightarrow BC \approx 978,5147\end{array}\)
Vậy khoảng cách giữa hai điểm ở hai đầu hồ là 978,5147 m.

tan x=\(\frac{150}{285}\)=\(\frac{10}{19}\) ➞ x\(\approx\) 27o46'
⇒⇒ Góc hạ của tia AB là 27o46′
Gọi độ cao của khinh khí cầu là y ⇒y=285.tan 46o \(\approx\) 295 m

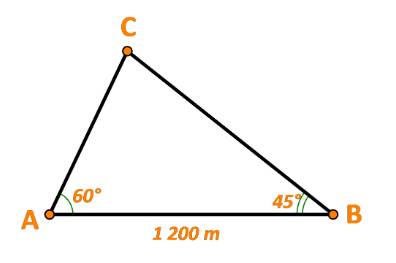
Ta có: \(\widehat C = {180^o} - {60^o} - {45^o} = {75^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \frac{{\sin B.AB}}{{\sin C}}\\BC = \frac{{\sin A.AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \frac{{\sin {{45}^o}.1200}}{{\sin {{75}^o}}} \approx 878\\BC = \frac{{\sin {{60}^o}.1200}}{{\sin {{75}^o}}} \approx 1076\end{array} \right.\)
Vậy AC = 878 m, BC = 1076 m.
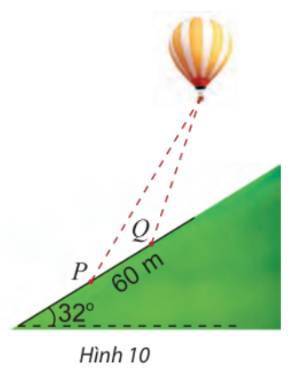



Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại P, góc nâng của khinh khí cầu là \({62^ \circ }\)\( \Rightarrow \widehat P = {62^ \circ } - {32^ \circ } = {30^ \circ }\)
Tại Q, góc nâng của khinh khí cầu là \({70^ \circ }\)\( \Rightarrow \widehat {AQt} = {70^ \circ } - {32^ \circ } = {38^ \circ }\)
\( \Rightarrow \widehat {AQP} = {180^ \circ } - {38^ \circ } = {142^ \circ }\) và \(\widehat A = {180^ \circ } - {142^ \circ } - {30^ \circ } = {8^ \circ }\)
Áp dụng định lí sin trong tam giác APQ, ta có:
\(\begin{array}{l}\frac{{PQ}}{{\sin A}} = \frac{{QA}}{{\sin P}}\\ \Rightarrow QA = \sin P.\frac{{PQ}}{{\sin A}} = \sin {30^ \circ }.\frac{{60}}{{\sin {8^ \circ }}} \approx 215,56\;(m)\end{array}\)
Vậy khoảng cách từ Q đến khinh khí cầu là 215,56 m.