Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Ta có :
\(64^2_1x=36x^2_2=48^2\)
=> \(64x_1\le48^2\)
=> \(36x_2\le48^2\)
=> A1 = 6 (cm)
=> A2 = 8 (cm)
=> \(\frac{V_2}{V_1}=\frac{\omega\sqrt{A^2_2-x^2_2}}{\omega\sqrt{A^2_1-x^2_1}}=\frac{\sqrt{A^2_2-x^2_2}}{\sqrt{A^2_1-x^2_1}}=\frac{4}{3\sqrt{3}}\)
Vậy V2 = \(\frac{4.18}{3\sqrt{3}}=8\sqrt{3}\) (cm/giây)

Gọi phương trình dao động là: \(x=A\cos\omega t\)
PT vận tốc là: \(v=x'=-\omega A\sin\omega t\)
Ta có: \(A\cos\omega t_0=2\)
Cần tìm:
\(v=-\omega A\sin\omega (t_0+0,5)\)
\(=-\omega A\sin(\omega .t_0+\dfrac{2\pi}{2}.0,5)\)
\(=-\omega A\sin(\omega .t_0+\dfrac{\pi}{2})\)
\(=-\dfrac{2\pi}{2} A\cos\omega t_0\)
\(=-\dfrac{2\pi}{2}.2=-2\pi(cm/s)\)
Chọn D

Áp dụng công thức: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow A^2=2,5^2+\dfrac{(50\sqrt 3)^2}{\omega^2}=(2,5\sqrt 3)^2+\dfrac{50^2}{\omega^2}\)
\(\Rightarrow \omega = 20(rad/s)\)
Và \(A=5cm\)

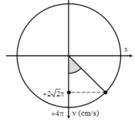
+ Vận tốc cực đại của dao động amax = ωA = 4π cm/s.
+ Tại thời điểm t = 0,25 vật có vận tốc
v = 2 2 v m a x = 2 π 2 cm/s
Thời điểm t = 0 ứng với góc lùi Δφ = ωΔt = 0,25π.
Biểu diễn các vị trí tương ứng trên đường tròn. Ta thu được: φ 0 = - π 2 rad
+ Phương trình dao động của vật
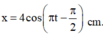
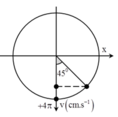
Đáp án C
 chọn A
chọn A
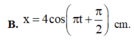
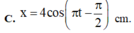
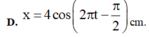


O A A' M N
Giả sử M và N là 2 vị trí của chất điểm ở thười điểm t1 và t2.Dễ thấy t2 hơn t1 \(1/4\) chu kì nên \(\widehat{MON}=90^o\Rightarrow\widehat{AOM}+\widehat{A'ON}=90^o\)
Ta có:\(\cos^2\widehat{AOM}+\cos^2\widehat{A'ON}=cos^2\widehat{AOM}+sin^2\widehat{AOM}=1\)
\(\Rightarrow\dfrac{x_1^2}{A^2}+\dfrac{x_2^2}{A^2}=1\). Kết hợp với \(A^2=x_1^2+\dfrac{v_1^2}{\omega^2}=x_2^2+\dfrac{v_2^2}{\omega^2}\)
\(\Rightarrow x_1^2=\dfrac{v_2^2}{\omega^2}\Rightarrow v_2=\left|x_1\right|.\dfrac{2\pi}{T}=4\pi\)(\(cm/s\))
Do chọn \(OA\equiv Ox\) làm chiều dương nên \(v_2\) sẽ dương