Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chuẩn hóa R = 1.
Gọi n là cảm kháng của cuộn dây khi tần số của dòng điện ω = ω 1 .
ω 1 2 = 1 L C ⇒ Z L 1 = n Z C 1 = n
Ta có cos φ = 0 , 707 = 1 1 2 + 2 n − n 2 2 ⇒ n = 2 3
Hệ số công suất khi ω = ω 3 là s φ = 1 1 2 + 3 2 n − 2 n 3 2 = 0 , 87
Đáp án A

Giải thích: Đáp án A
Phương pháp: Chu n hoá số liệu
Cách giải:
+ Ta có:
| f |
ZL |
ZC |
cosφ |
| 60Hz |
1 |
a |
|
| 120Hz |
2 |
a/2 |
|
| 180Hz |
3 |
a/3 |
|
| 30Hz |
1/2 |
2a |
|
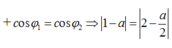

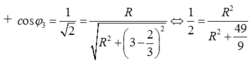


Đáp án A
+ Khi ω = ω 1 mạch xảy ra cộng hưởng, ta chuẩn hóa R = 1, Z L 1 = Z C 1 = n .
+ Khi ω = ω 2 = 2 ω 1
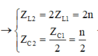
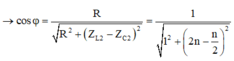
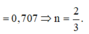
+ Khi ω = ω 3 = 1 , 5 ω 1
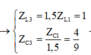
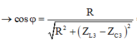
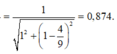

Đáp án D
Ta chuẩn hóa số liệu:
+ f =
f
1
= 60 Hz: Đặt R = 1 thì 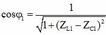
+ f =
f
2
= 120 Hz: có ![]()
![]()
+ f =
f
3
= 180 Hz: có![]()
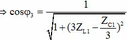
Theo đề bài: 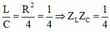
![]()
Có ![]()
![]()
Từ (1) và (2) tìm được  Thay vào cos
φ
3
= 0,923
Thay vào cos
φ
3
= 0,923

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

Đáp án D
+ Chuẩn hóa 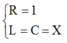
+ Hai giá trị của tần số góc cho cùng giá trị công suất
: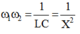
+ Tần số góc để điện hấp hiệu dụng ở hai đầu cuộn cảm đạt cực đại:

Ta có: 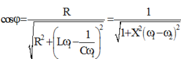
Mặc khác
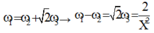
→ Thay vào biểu thức trên ta thu được
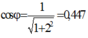
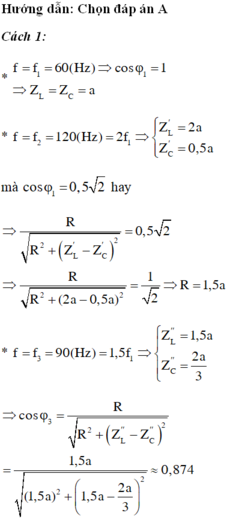
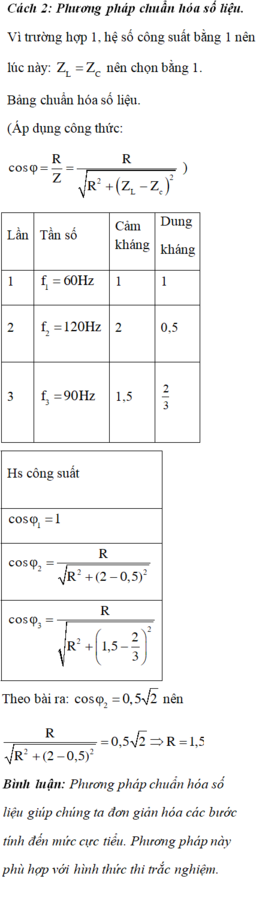



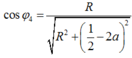
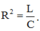

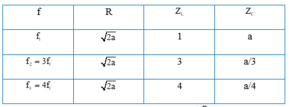

\(f_1=60Hz , cos\varphi=1 \Rightarrow Z_{L1}=Z_{C1}\)
\(f_2=120Hz=2f_1 \Rightarrow Z_{L2}=2Z_{L1}; Z_{C2}=0,5Z_{C1}=0,5Z_{L1}\)
\(\Rightarrow cos\varphi_2=\frac{R}{\sqrt{R^2+\left(Z_{L2}-Z_{C2}\right)^2}}=\frac{R}{\sqrt{R^2+\left(2Z_{L1}-0,5Z_{C1}\right)^2}}=\frac{R}{\sqrt{R^2+\left(2Z_{L1}-0,5Z_{L1}\right)^2}}=\frac{R}{\sqrt{R^2+\left(1,5Z_{L1}\right)^2}}=0,707\)\(\Rightarrow Z_{L1}=\frac{R}{1,5}\)(*)
\(f_3=90Hz=1,5f_1\Rightarrow Z_{L3}=1,5Z_{L1};Z_{C3}=\frac{Z_{C1}}{1,5}=\frac{Z_{L1}}{1,5}\)
\(\Rightarrow cos\varphi_3=\frac{R}{\sqrt{R^2+\left(Z_{L3}-Z_{C3}\right)^2}}=\frac{R}{\sqrt{R^2+\left(1,5Z_{L1}-\frac{Z_{L1}}{1,5}\right)^2}}\)(**)
Thay (*) vao (**)\(\Rightarrow cos\varphi_3=\frac{R}{\sqrt{R^2+\left(1,5.\frac{R}{1,5}-\frac{R}{\left(1,5\right)^2}\right)^2}}=\frac{R}{\sqrt{R^2+\frac{25}{81}R^2}}\approx0,874\)
=>A
bạn ơi cho mình hỏi sao mà suy ra đc Zl2= 2 Zl1 và Zc2= 0,5 Zc1= o,5 Zl1 vậy