Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1 :
Phương trình a z 2 + bz + c = 0 có Δ = b 2 - 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức 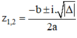
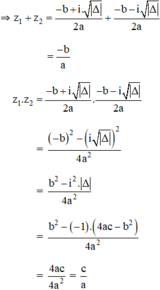
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
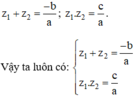
Cách 2 :

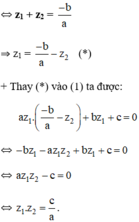

Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)( x 2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3 π /2

Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)( x 2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3π/2.

a) Gọi \(z_1,z_2\) là các nghiệm của phương trình với \(\left|z_1\right|=1\). Từ \(z_2=\frac{c}{a}.\frac{1}{z_1}\) kéo theo \(\left|z_2\right|=\left|\frac{c}{a}\right|.\frac{1}{\left|z_1\right|}=1\)
vì \(z_1+z_2=-\frac{b}{a},\left|a\right|=\left|b\right|\), ta có \(\left|z_1+z_2\right|^2=1\)
Hệ thức tương đương với
\(\left(z_1+z_2\right)\left(\overline{z_1}+\overline{z_2}\right)=1\) tức là \(\left(z_1+z_2\right)\left(\frac{1}{z_1}+\frac{1}{z_2}\right)=1\)
\(\left(z_1+z_2\right)^2=z_1z_2\)
hay \(\left(-\frac{b}{a}\right)^2=\frac{c}{a}\Rightarrow b^2=ac\)
b) Theo câu a) \(b^2=ac,c^2=ab\). Nhân các hệ thức được \(b^2c^2=a^2bc\Rightarrow a^2=bc\)
Do đó \(a^2+b^2+c^2=ab+bc+ca\)
Hệ tương đương với :
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Tức là
\(\left(a-b\right)^2+\left(b-c\right)^2+2\left(a-b\right)\left(b-c\right)+\left(c-a\right)^2=2\left(a-b\right)\left(b-c\right)\)
Kéo theo
\(\left(a-c\right)^2=\left(a-b\right)\left(b-c\right)\)
Lấy giá trị tuyệt đối, được \(\beta^2=\gamma\alpha\)
Ở đây \(\alpha=\left|b-c\right|,\beta=\left|c-a\right|,\gamma=\left|a-b\right|\)
Tương tự được :
\(\alpha^2=\beta\gamma,\gamma^2=\alpha\beta,\)
Cộng các hệ thức, được :
\(\alpha^2+\beta^2+\gamma^2=\alpha\beta+\beta\gamma+\gamma\alpha\)
Tức là (\(\left(\alpha-\beta\right)^2+\left(\beta-\gamma\right)^2+\left(\gamma-\beta\right)^2=0\)
Do đó : \(\beta=\alpha=\gamma\)

Đặt \(z_1=x+yi\Rightarrow z_2=x-yi\)
\(\Rightarrow z_1z_2=x^2+y^2\)
\(\left|z_1^2\right|+\left|z_2^2\right|=10\Leftrightarrow\left|\left(x+yi\right)^2\right|+\left|\left(x-yi\right)^2\right|=10\)
\(\Leftrightarrow\left|x^2-y^2+2xyi\right|+\left|x^2-y^2-2xyi\right|=10\)
\(\Leftrightarrow\sqrt{\left(x^2-y^2\right)^2+4x^2y^2}+\sqrt{\left(x^2-y^2\right)^2+4x^2y^2}=10\)
\(\Leftrightarrow\left(x^2-y^2\right)^2+4x^2y^2=25\)
\(\Leftrightarrow\left(x^2+y^2\right)^2=25\)
\(\Leftrightarrow x^2+y^2=5\)

Toàn bộ nghiệm của 3 pt này đều là nghiệm thực, không có nghiệm phức nào
a. \(x^2-3x-2=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{17}}{2}\\x=\dfrac{3-\sqrt{17}}{2}\end{matrix}\right.\)
b. \(x^4-5x^2+6=0\Rightarrow\left[{}\begin{matrix}x^2=2\\x^2=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x=\pm\sqrt{3}\end{matrix}\right.\)
c. \(-x^2+4x+5=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=5\end{matrix}\right.\)

Chọn A.
Ta có: z1 = 3 + i; z2 = 1 - 2i là 2 nghiệm của phương trình đã cho và z1 + z2 = 4 - i (1)
Theo Viet, ta có:
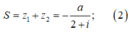
Từ (1) và (2) suy ra: