Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bất đẳng thức tam giác:
a) Vì 2 + 3 = 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thể là độ dài ba cạnh của một tam giác
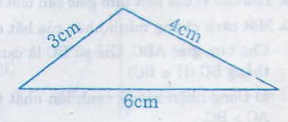
b) Vì 3+4 > 6 nên bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác

* Cách vẽ: + Vẽ độ dài cạnh AB = 6cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 3 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
c) Vì 2+4 > 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm có thể là độ dài ba cạnh của một tam giác
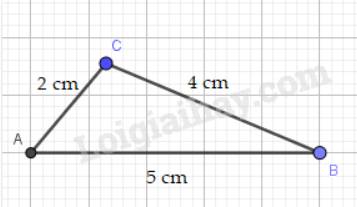
* Cách vẽ: + Vẽ độ dài cạnh AB = 5cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 2 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.

a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
a) Nhận xét: 2cm + 3cm = 5cm < 6cm nên bộ ba đoạn thẳng dài 2cm, 3cm, 6cm không phải là bộ ba cạnh của một tam giác.
b) Nhận xét: 2cm + 4cm = 6cm = 6cm nên bộ ba đoạn thẳng dài 2cm, 4cm, 6cm không phải là bộ ba cạnh của một tam giác.
c) Nhận xét: 3cm + 4cm = 7cm > 6cm nên bộ ba đoạn thẳng dài 3cm, 4cm, 6cm là bộ ba cạnh của một tam giác.


Giải:
Gọi 3 cạnh của tam giác ABC lần lượt là a, b, c ( a > b > c > 0 )
Ta có: \(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}\) và a - c = 10
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}=\frac{a-c}{5-3}=\frac{10}{2}=5\)
+) \(\frac{a}{5}=5\Rightarrow a=25\)
+) \(\frac{b}{4}=5\Rightarrow b=20\)
+) \(\frac{c}{3}=5\Rightarrow c=15\)
Vậy 3 cạnh của tam giác lần lượt là 15 cm, 20 cm và 25 cm
Gọi độ dài các cạnh của tam giác lần lượt là a , b , c (theo thứ tự nhỏ đến lớn)
Theo đề bài , ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và c + 10 = a + b
Áp dụng tính chất dãy tỉ số bằng nhau , ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{a+b}{3+4}=\frac{c+10}{7}\)
=> \(\frac{c+10}{7}=\frac{c}{5}\)
=> 5(c + 10) = 7c
=> 5c + 50 = 7c
=> 50 = 2c
=> c = 25
=> a + b = 25 + 10 = 35
Áp dụng tính chất dãy tỉ số , ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{a+b}{3+4}=\frac{35}{7}=5\)
=> a = 3.5 = 15
b = 4.5 = 20

a) Ta thấy:
\(\begin{array}{l}8 - 5 = 3 = 3\end{array}\)
Vậy bộ ba số đo độ dài 8 cm, 5 cm, 3 cm không thể là độ dài ba cạnh của một tam giác.
b) Ta thấy:
\(\begin{array}{l}12 - 6 = 6\end{array}\)
Vậy bộ ba số đo độ dài 12 cm, 6 cm, 6 cm không thể là độ dài ba cạnh của một tam giác.
c) Ta thấy: \(15 - 9 = 6 > 4\).
Vậy bộ ba số đo độ dài 15 cm, 9 cm, 4 cm không thể là độ dài ba cạnh của một tam giác.

2: BC=căn 6^2+8^2=10cm
3:
a: 5cm; 12cm; 9cm
5+12>9; 5+9>12; 12+9>5
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
b: 12+16>20; 12+20>16; 20+16>12
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
4:
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
10:
a: AB=căn 10^2-6^2=8cm
b: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
c: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>AB//CD

Gọi tam giác đó là \(\Delta\)ABC.AB = 4 cm
AC= 7cm
BC = 8cm
Ta có \(AB^2+AC^2\)=16+49=65 cm
Lại có \(BC^2\)=64
Mà 65\(\ne\)64
\(\Rightarrow\)\(AB^2+AC^2\ne BC^2\)
\(\Delta\)ABC \(K^o\)phải là tam giác vuông (định lí Pi-ta-go) (đpcm)
hok tốt

Ta có: 2,5 + 3,4 = 5,9 cm < 6 cm nên không có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm.

a) Có, vì 12 < 5 + 10.
b) Không, vì 1 + 2 = 3
c) Có, vì 9 < 6 + 8.
a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.
b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác