DN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
0
6 tháng 10 2021
\(1)4x^2-25+\left(2x+7\right).\left(5.2x\right)\)
\(=\left(2x\right)^2-5^2-\left(2x+7\right).\left(2x-5\right)\)
\(=\left(2x.5\right)\left(2x+5\right).\left(2x+7\right)\left(2x-5\right)\)
\(=\left(2x-5\right)\left(2x+5-2x+7\right)\)
\(=\left(2x-5\right).12\)
\(2)3x+4-x^2-4x\)
\(=3(x+4)-\left(x+4\right)\)
\(=\left(3-x\right)\left(x+4\right)\)
\(3)5x^2-2y^2-10x+10y\)
\(=5\left(x^2-y^2\right)-10\left(x-4\right)\)
\(=5\left(x-y\right)\left(x+y\right)-10\left(x-y\right)\)
\(=\left(x-y\right)[5(x+y)-10]\)
Còn lại bn lm nốt nha!
12 tháng 7 2021
Ta có: \(5x^2-10x+2x-4\)
\(=5x\left(x-2\right)+2\left(x-2\right)\)
=(x-2)(5x+2)
H9
HT.Phong (9A5)
CTVHS
19 tháng 10 2023
\(4x^4+4x^3+5x^2+2x+1\)
\(=4x^4+2x^3+2x^2+2x^3+x^2+2x^2+x+1\)
\(=2x^2\left(2x^2+x+1\right)+x\left(2x^2+x+1\right)+\left(2x^2+x+1\right)\)
\(=\left(2x^2+x+1\right)\left(2x^2+x+1\right)\)
\(=\left(2x^2+x+1\right)^2\)
S
27 tháng 8 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
DN
0
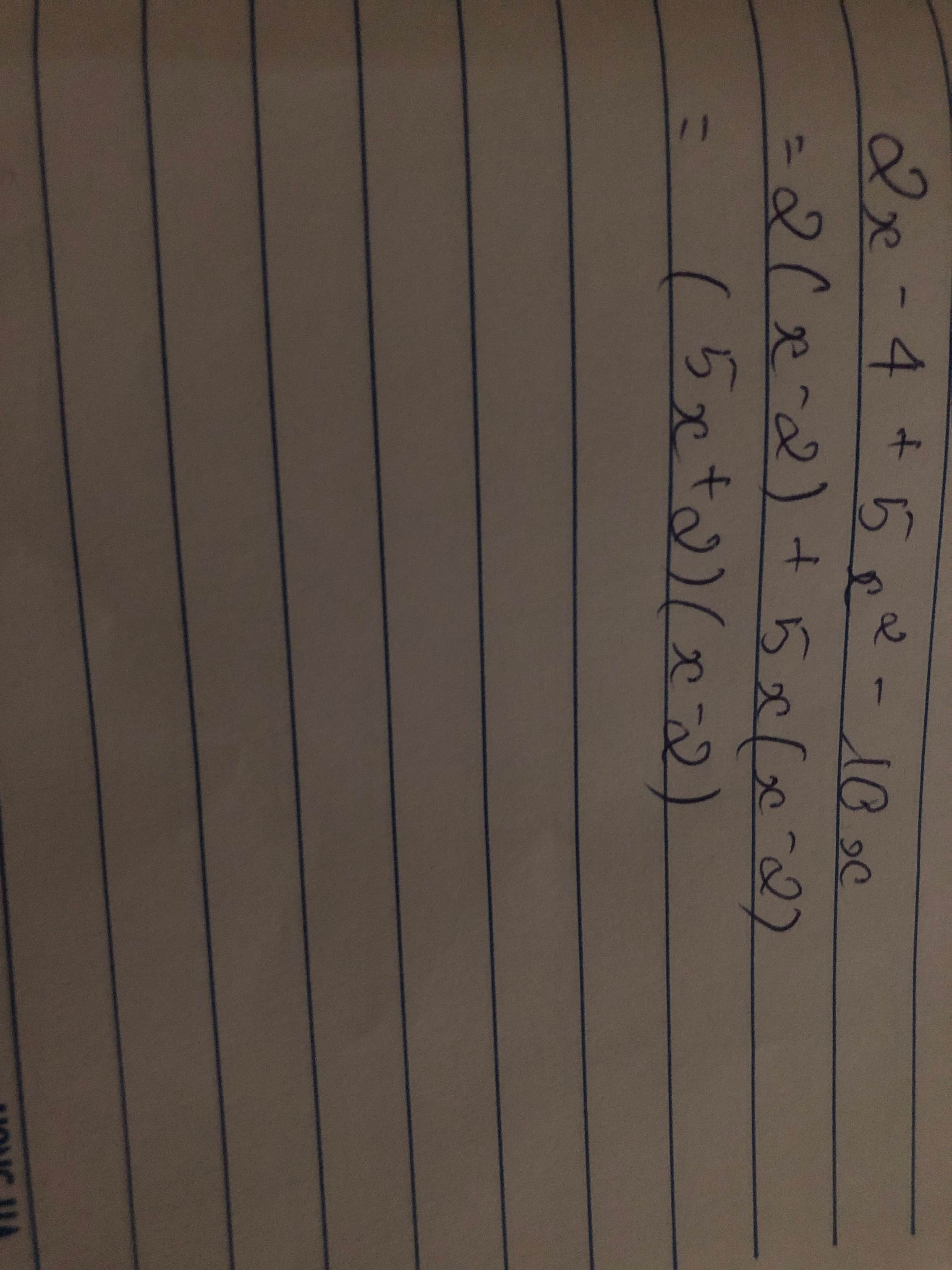
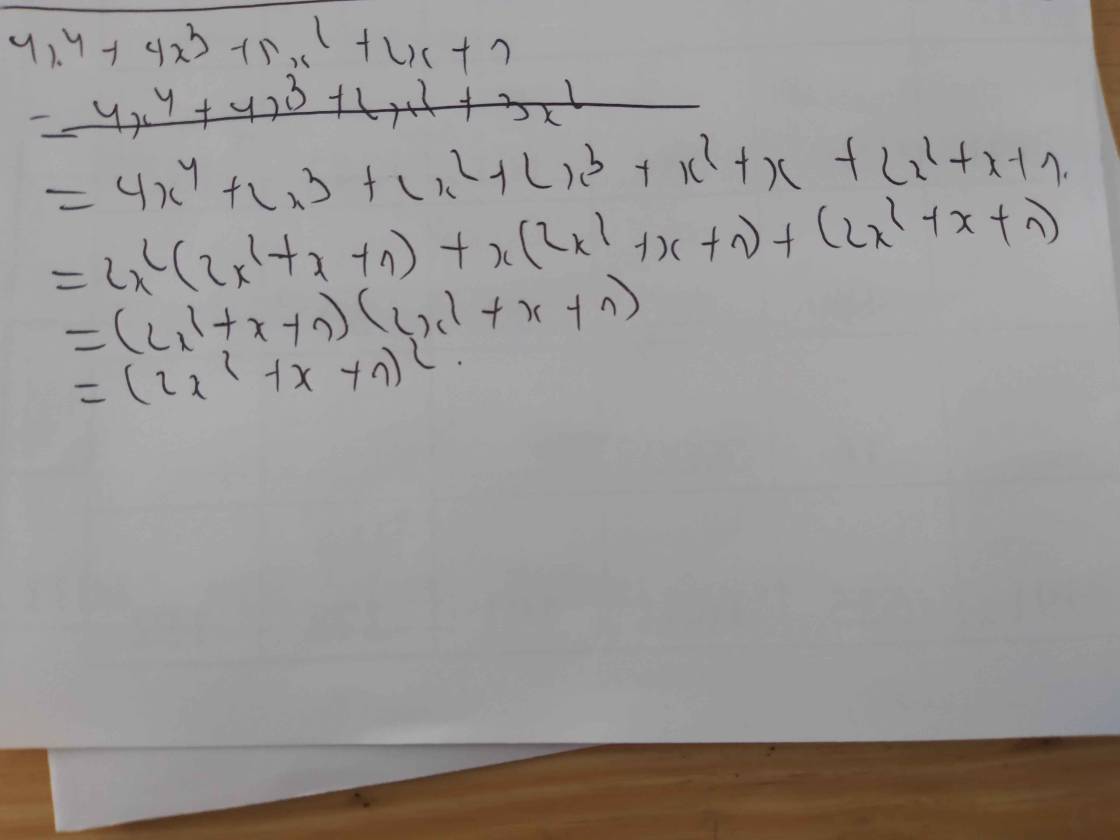
[(10x+4).(2x+1)].[(4x-2).(5x+7)] + 17 = (20x + 18x + 4)(20x + 18x - 14) + 17.
Đến đây ta đặt 20x + 18x - 5 = t, ta được: (t - 9)(t + 9) + 17 = 0 \(\Leftrightarrow\) t2 - 81 + 17 = 0
Đến đây bạn tự làm tiếp nhé!