
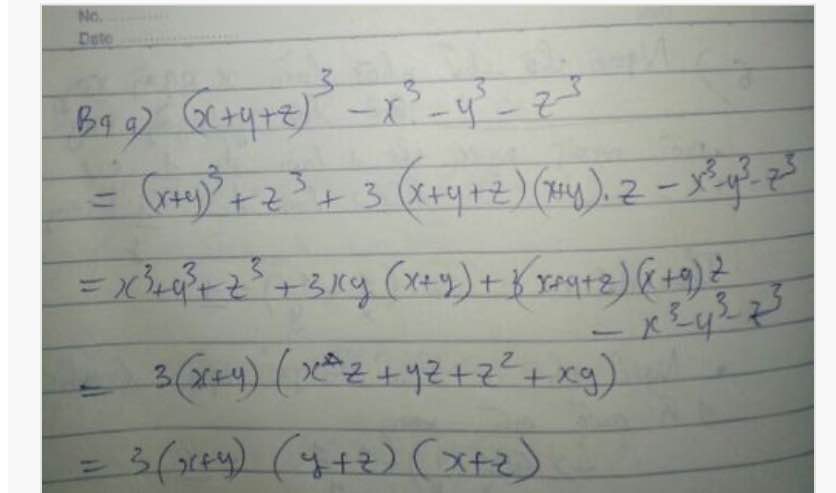
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

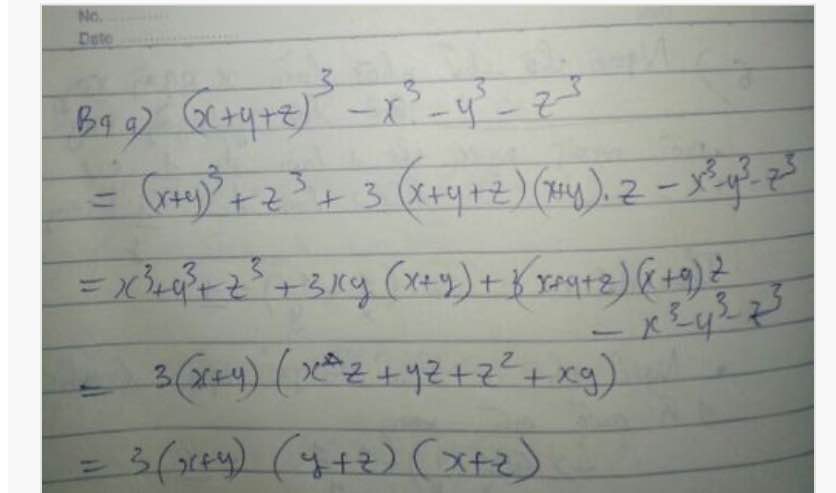

Đặt \(x+y-z=a;x-y+z=b;y+z-x=c\)
Ta có:\(A=\left(a+b+c\right)^3-a^3-b^3-c^3\)
\(A=\left[\left(a+b\right)+c\right]^3-a^3-b^3-c^3\)
\(A=\left(a+b\right)^3+3\left(a+b\right)\cdot c\cdot\left(a+b+c\right)+c^3-a^3-b^3-c^3\)
\(A=a^3+b^3+3ab\left(a+b\right)+3\left(a+b\right)c\left(a+b+c\right)+c^3-a^3-b^3-c^3\)
\(A=3\left(a+b\right)\left(ab+ac+bc+c^2\right)\)
\(A=3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Hay \(A=3\cdot2x\cdot2y\cdot2z\)
\(A=24xyz\)



Ta có :
\(\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=\left[\left(x+y+z\right)^3-x^3\right]-\left(y^3+z^3\right)\)
\(=\left(x+y+z-x\right)\left[\left(x+y+z\right)^2+x^2+\left(x+y+z\right)x\right]-\left(y+z\right)\left(y^2+z^2-yz\right)\)
\(=\left(y+z\right)\left[x^2+y^2+z^2+2\left(xy+yz+xz\right)+x^2+x^2+xy+zx\right]\)\(-\left(y+z\right)\left(y^2+z^2-yz\right)\)
\(=\left(y+z\right)\left[3x^2+y^2+z^2+3xy+3zx+2yz-y^2-z^2+yz\right]\)
\(=\left(y+z\right)\left[3x^2+3xy+3zx+3yz\right]\)
\(=\left(y+z\right)3\left[\left(x^2+xy\right)+\left(zx+yz\right)\right]\)
\(=3\left(y+z\right)\left(x+y\right)\left(x+z\right)\)
Vậy ...

\(\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=x^3+y^3+z^3+2xy+2xz+2yz-x^3-y^3-z^3\)
\(=2xy+2xz+2yz\)
\(=2\left(xy+xz+yz\right)\)
Đc chưa ?
Phương Đỗ Sai rùi bạn.
\(\left(x+y+z\right)^3-x^3-y^3-z^3\)
\(=\left[\left(x+y\right)+z\right]^3-x^3-y^3-z^3\)
\(=\left(x+y\right)^3+3\left(x+y+z\right)\left(x+y\right)z+z^3-x^3-y^3-z^3\)
\(=x^3+y^3+3xy\left(x+y\right)+3\left(x+y+z\right)\left(x+y\right)z+z^3-x^3-y^3-z^3\)
\(=3xy\left(x+y\right)+3\left(x+y+z\right)\left(x+y\right)z\)
\(=3\left(x+y\right)\left(xy+xz+yz+z^2\right)\)
\(=3\left(x+y\right)\left(y+z\right)\left(z+x\right)\)