Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

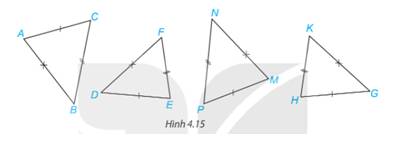
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)

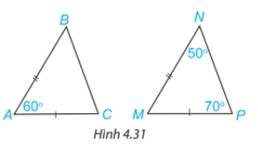
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Do hai tam giác trên có hai cặp góc bằng nhau nên cặp góc còn lại bằng nhau.
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\widehat A = \widehat {A'}\) (gt)
AC = A'C' (gt)
\(\widehat C = \widehat {C'}\) (cmt)
\(\Rightarrow \Delta ABC = \Delta A'B'C'\) (g.c.g)
Vậy hai tam giác đã cho bằng nhau theo trường hợp góc – cạnh – góc.

Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau ( g-c-g)

Khi hai tam giác có thể trồng khít lên nhau thì các cạnh tương ứng của hai tam giác bằng nhau và các góc tương ứng của hai tam giác bằng nhau.

Em thấy bạn Vuông nói đúng
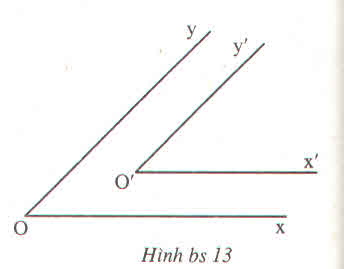
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
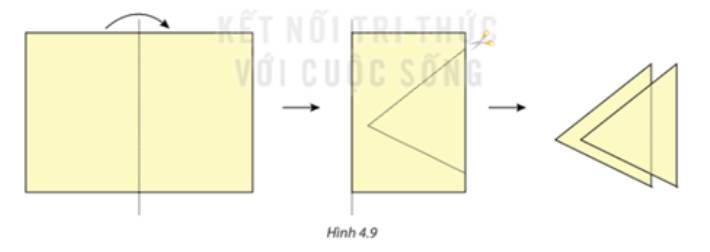






Quan sát hình vẽ ta thấy:
- Các cạnh tương ứng bằng nhau.
- Các góc tương ứng bằng nhau.