Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quan sát hình vẽ ta thấy:
- Các cạnh tương ứng bằng nhau.
- Các góc tương ứng bằng nhau.

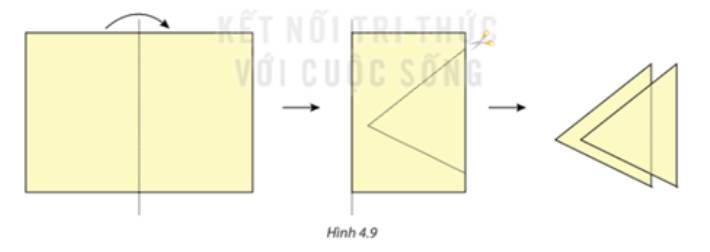
Ba góc tại mỗi đỉnh chung của ba tam giác tạo thành góc bẹt
Do đó, tổng của chúng bằng 180 độ.
Ta thấy ba điểm A, B, C thẳng hàng.

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

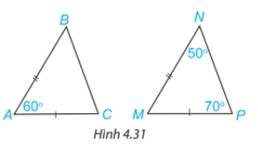
Xét tam giác MNP có:
\(\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow \widehat M + {50^o} + {70^o} = {180^o}\\ \Rightarrow \widehat M = {60^o}\end{array}\)
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP} (=60^0)\)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

Xem hình a) ta có:
\(\widehat{A}=\widehat{I}=80^0\) ; \(\widehat{C}=\widehat{N}=30^0\)
\(\widehat{B}=\widehat{M}=180^0-\left(80^0+30^0\right)=70^0\)
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
\(\widehat{Q}_2=\widehat{R}_2=80^0\)=800 (ở vị trí so le trong)
Nên QH// RP
Nên \(\widehat{R}_1=\widehat{Q}_1\)= 600(so le trong)
\(\widehat{P}=\widehat{H}\)= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.
Xem hình a) ta có:
ˆAA^=ˆII^=800,ˆCC^=ˆNN^=300
ˆBB^=ˆMM^=1800-(800+300)=700
Và AB=MI, AC=IN, BC=MN.
nên ∆ABC=∆IMN
Xem hình b) ta có:
ˆQ2Q2^=ˆR2R2^=800 (ở vị trí so le trong)
Nên QH// RP
Nên ˆR1R1^ = ˆQ1Q1^= 600(so le trong)
ˆPP^=ˆHH^= 400
và QH= RP, HR= PQ, QR chung.
nên ∆HQR=∆PRQ.

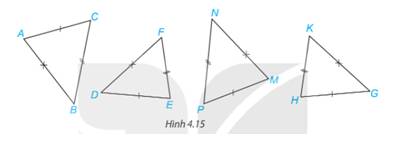
Xét \(\Delta ABC\) và \(\Delta MNP\) có:
\(\begin{array}{l}AB = MN\\BC = NP\\AC = MP\end{array}\)
Vậy\(\Delta ABC\) =\(\Delta MNP\)(c.c.c)
Xét \(\Delta DEF\) và \(\Delta GHK\) có:
\(\begin{array}{l}DE = GH\\EF = HK\\DF = GK\end{array}\)
Vậy\(\Delta DEF\)=\(\Delta GHK\) (c.c.c)




Khi hai tam giác có thể trồng khít lên nhau thì các cạnh tương ứng của hai tam giác bằng nhau và các góc tương ứng của hai tam giác bằng nhau.