Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cố định 3 tem thư xếp theo hàng ngang từ trái sang phải là các vị trí 1, 2, 3.
Rõ ràng nếu có 3 bì thư thì mỗi thứ tự xếp 3 bì thư này từ trái sáng phải cũng chính là cách dán.
Số cách làm cần tìm là ![]()
Chọn D.

Trong không gian mẫu \(\Omega\) là tập hợp gồm tất cả các cặp hai bộ 3 câu hỏi, mà ở vị trí thứ nhất của cặp là bộ 3 câu hỏi thí sinh A chọn và ở vị trí thứ hai của cặp là bộ 3 câu hỏi thí sinh B chọn
Vì A cũng như B đều có \(C_{10}^3\) cách chọn 3 câu hỏi tứ 10 câu hỏi thí sinh nên theo quy tắc nhân ta có \(n\left(\Omega\right)=\left(C_{10}^3\right)^2\)
Kí hiệu X là biến cố " bộ 3 câu hỏi A chọn và bộ 3 câu hỏi B chọn là giống nhau"
Vì mỗi cách chọn 3 câu hỏi của A, B chỉ có duy nhất cách chọn 3 câu hỏi giống như A nên \(n\left(\Omega_X\right)=C_{10}^3.1=C_{10}^3\)
Vì vậy \(P\left(X\right)=\frac{n\left(\Omega_X\right)}{n\left(\Omega\right)}=\frac{C^3_{10}}{\left(C^3_{10}\right)^2}=\frac{1}{C^3_{10}}=\frac{1}{120}\)

1) \(C^3_8.C^3_6=1120cách\)
2) Lấy 1 đỉnh bất kì có n cách
Nối đỉnh đó với n-1 đỉnh còn lại ta được n-1 đoạn
Trong n-1 đoạn đó có 2 đoạn kề nhau là cạnh của tứ giác nên có n-3 đường chéo
Mỗi đường chéo tính 2 lần -> có\(\frac{n\left(n-3\right)}{2}\)đường chéo
Thay n=20 -> đa giác có 170 đường chéo
3) Có\(C^{10}_{20}cách\)

- Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 3! = 6\)
- Gọi B là biến cố “Không lá thư nào được bỏ đúng phong bì”
A là biến cố “Có ít nhất một lá thư được bỏ đúng phong bì”
⇨ n(B) = 2
⇨ \(P(A) = 1 - P(B) = 1 - \frac{2}{6} = \frac{2}{3}\)
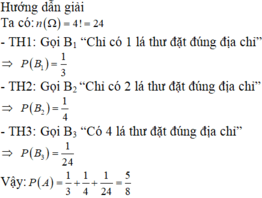
Có 5 bì thư khác nhau, chọn 3 bì thư có C53 cách chọn
Có 8 tem khác nhau, chọn 3 con tem thì có C83 cách chọn
Dán 3 con tem lên 3 bì thư thì có 3!cách dán khác nhau. Theo quy tắc nhân ta có 3!C53.C83 cách dán 3 con tem lên 3 bì thư (chọn đáp án D)
Nhận xét: học sinh có thể nhầm lẫn: số cách chọn 3 bì thư là A53, số cách chọn 3 con tem là A83 hoặc không tính cách dán 3 con tem lên 3 bì thư dẫn đến có thể chọn các phương án A, B và C.
Chọn D