
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Em tham khảo tại đây nhé:
Câu hỏi của VRCT_Ran love shinichi - Toán lớp 8 - Học toán với OnlineMath

\(A=n^4+6n^3+11n^2+6n\)
\(=n\left(n^3+6n^2+11n+6\right)\)
\(=n\left(n^3+n^2+5n^2+5n+6n+6\right)\)
\(=n\left[n^2\left(n+1\right)+5n\left(n+1\right)+6\left(n+1\right)\right]\)
\(=n\left(n+1\right)\left(n^2+5n+6\right)\)
\(=n\left(n+1\right)\left(n+2\right)\left(n+3\right)\)
Do đây là tích 4 số nguyên liên tiếp nên nó vừa chia hết cho \(2,3,4\Rightarrow A\) chia hết cho 24

bạn sai đề rồi:
chứng minh với mọi số nguyên n thì n^2+11n+39 không chia hết cho 49
Ta có:
giả sử: A= n^2 + 11n + 39 chia hết cho 49 => A chia hết cho 7
mà : n^2 + 11n + 39 = (n+9)(n+2) +21 chia hết cho 7
=> (n+9)(n+2) chia hết cho 7
lại có: (n+9) - (n+2) = 7 nên (n+9) và (n+2) đồng thời chia hết cho 7
=>(n+9)(n+2) chia hết cho 49
mà: (n+9)(n+2) +21 chia hết cho 49
=> 21 chia hết cho 49 vô lí => đpcm
https://vn.answers.yahoo.com/question/index?qid=20091017203207AAoSfKD
ban vao link nay thi se co cau tra loi

\(n^2+5n+15⋮49\)
\(\Rightarrow n^2+5n+15⋮7\)
\(\Leftrightarrow n^2-2n+1=\left(n-1\right)^2⋮7\)
\(\Leftrightarrow n-1⋮7\)
\(\Leftrightarrow n=7k+1,k\inℕ\).
\(n^2+5n+15=\left(7k+1\right)^2+5\left(7k+1\right)+15\)
\(=49k^2+49k+6⋮̸49\).
Ta có đpcm.


CM bằng cách thế số vào n
Thay n=169,ta đc
1692+11.169+2=30422
Ta thấy : 30422 ko chia hết cho 12769
\(\Rightarrow\)\(n^2+11n+2\)ko chia hết cho 12769 với mọi n

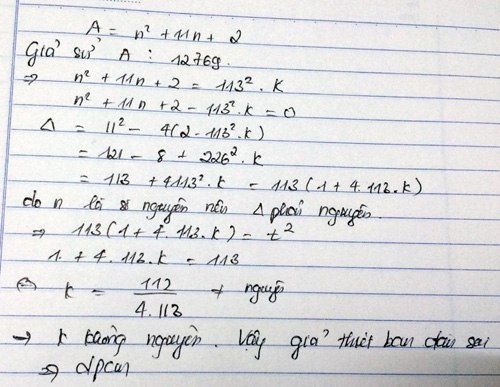
chứng minh nó không chia hết cho 49 là được. dễ mà
Đặt A=n2+11n+39
Giả sử n2+11n+39 chia hết cho 49 thì A chia hết cho 49 => A cũng chia hết cho 7
Ta có A=n2+11n+39=n2+9n+2n+18+21 = n(n+9)+2(n+9)+21 =(n+9)(n+2)+21
Nhận thấy( n+9)-(n+2)=7
=>Đồng thời (n+9) và (n+2) chia hết cho 7 => (n+9)(n+2) chia hết cho 49
Ta cũng có A chia hết cho 49 mà 21 ko chia hết cho 49 ( vô lí )
Vậy n2+11n+39 ko chia hết cho 49