Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
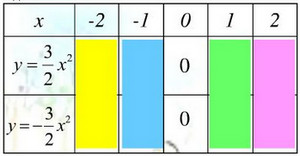
Vẽ đồ thị:
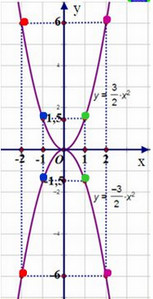
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO

a) Ta có y=f(x)=−1/2x+3y=f(x)=−1/2x+3.
Với y=−1/2x+3y=−1/2x+3 thay các giá trị của xx vào biểu thức của yy, ta được:
+) f(−2,5)=−1/2.(−2,5)+3f(−2,5)=−1/2.(−2,5)+3
=(−0,5).(−2,5)+3=(−0,5).(−2,5)+3=1,25+3=4,25=1,25+3=4,25
+) f(−2)=−1/2.(−2)+3f(−2)=−1/2.(−2)+3
=(−0,5).(−2)+3=1+3=4=(−0,5).(−2)+3=1+3=4.
+) f(−1,5)=−1/2.(−1,5)+3f(−1,5)=−1/2.(−1,5)+3
=(−0,5).(−1,5)+3=(−0,5).(−1,5)+3=0,75+3=3,75=0,75+3=3,75.
+) f(−1)=−1/2.(−1)+3f(−1)=−1/2.(−1)+3
=(−0,5).(−1)+3=0,5+3=3,5=(−0,5).(−1)+3=0,5+3=3,5.
+) f(−0,5)=−1/2.(−0,5)+3f(−0,5)=−1/2.(−0,5)+3
=(−0,5).(−0,5)+3=(−0,5).(−0,5)+3=0,25+3=3,25=0,25+3=3,25.
+) f(0)=−1/2.0+3f(0)=−1/2.0+3=(−0,5).0+3=0+3=3=(−0,5).0+3=0+3=3
+) f(0,5)=−1/2.0,5+3f(0,5)=−1/2.0,5+3
=(−0,5).0,5+3=(−0,5).0,5+3=−0,25+3=2,75=−0,25+3=2,75
+) f(1)=−1/2.1+3f(1)=−1/2.1+3
=(−0,5).1+3=−0,5+3=2,5=(−0,5).1+3=−0,5+3=2,5.
+) f(1,5)=−1/2.1,5+3f(1,5)=−1/2.1,5+3
=(−0,5).1,5+3=−0,75+3=(−0,5).1,5+3=−0,75+3=2,25=2,25
+) f(2)=−1/2.2+3f(2)=−1/2.2+3
=(−0,5).2+3=−1+3=2=(−0,5).2+3=−1+3=2.
+) f(2,5)=−1/2.2,5+3f(2,5)=−1/2.2,5+3
=(−0,5).2,5+3=−1,25+3=(−0,5).2,5+3=−1,25+3=1,75=1,75
Ta có bảng sau:

b)
Nhìn vào bảng giá trị của hàm số ở câu a ta thấy khi xx càng tăng thì giá trị của f(x)f(x) càng giảm. Do đó hàm số nghịch biến trên R
a)
| xx | -2,5−2,5 | -2−2 | -1,5−1,5 | -1−1 | -0,5−0,5 | 00 | 0,50,5 | 11 | 1,51,5 | 22 | 2,52,5 |
| y=-\dfrac{1}{2} x+3y=− \(\dfrac{1}{2}\)x+3 |
4,254,25 | 44 | 3,753,75 | 3,53,5 | 3,253,25 | 33 | 2,752,75 | 2,52,5 | 2,252,25 | 22 | 1,751,75 |
b) Khi xx lần lượt nhận các giá trị tăng lên thì giá trị tương ứng của hàm số lại giảm đi. Vậy hàm số đã cho nghịch biến trên \mathbb{R}R.

\(6\left(x^2+y^2+z^2\right)+10\left(xy+yz+xz\right)+2\left(\dfrac{1}{2x+y+z}+\dfrac{1}{x+2y+z}+\dfrac{1}{x+y+2z}\right)\)
\(=6\left(x^2+y^2+z^2\right)+12\left(xy+yz+xz\right)+2\left(\dfrac{1}{2x+y+z}+\dfrac{1}{x+2y+z}+\dfrac{1}{x+y+2z}\right)-2\left(xy+yz+xz\right)\)
\(=6\left(x+y+z\right)^2+2\left(\dfrac{1}{2x+y+z}+\dfrac{1}{x+2y+z}+\dfrac{1}{2z+x+y}\right)-2\left(xy+yz+xz\right)\)
\(\ge6\left(x+y+z\right)^2+2.\dfrac{\left(1+1+1\right)^2}{2x+y+z+x+2y+z+2z+x+y}-2\left(xy+yz+xz\right)\)
\(=6\left(x+y+z\right)^2+\dfrac{18}{4\left(x+y+z\right)}-2\left(xy+yz+xz\right)\)
\(\ge6\left(x+y+z\right)^2+\dfrac{18}{4\left(x+y+z\right)}-\dfrac{2}{3}\left(x+y+z\right)^2\)
\(=6.\left(\dfrac{3}{4}\right)^2+\dfrac{18}{4.\dfrac{3}{4}}-\dfrac{2}{3}.\left(\dfrac{3}{4}\right)^2=9\)
\("="\Leftrightarrow x=y=z=\dfrac{1}{4}\)
a) ab+bc+ca\(\le\dfrac{\left(a+c+b\right)^2}{3}\)
\(\Leftrightarrow3ab+3bc+3ac\le a^2+b^2+c^2+2ab+2bc+2ac\)
\(\Leftrightarrow ab+bc+ac\le a^2+b^2+c^2\)
\(\Leftrightarrow2ab+2bc+2ca\le2a^2+2b^2+2c^2\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2\ge0\)
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) (luôn đúng \(\forall a,b,c\)

Lời giải:
Điều kiện: $a,b,c>0$
Áp dụng BĐT Cauchy-Schwarz ta có:
\(\frac{a+b}{ab+c^2}=\frac{(a+b)^2}{(ab+c^2)(a+b)}=\frac{(a+b)^2}{a(b^2+c^2)+b(a^2+c^2)}\leq \frac{b^2}{a(b^2+c^2)}+\frac{a^2}{b(a^2+c^2)}\)
\(\frac{b+c}{bc+a^2}=\frac{(b+c)^2}{(b+c)(bc+a^2)}=\frac{(b+c)^2}{c(b^2+a^2)+b(a^2+c^2)}\leq \frac{b^2}{c(a^2+b^2)}+\frac{c^2}{b(a^2+c^2)}\)
\(\frac{c+a}{ca+b^2}=\frac{(c+a)^2}{(c+a)(ac+b^2)}=\frac{(c+a)^2}{c(a^2+b^2)+a(b^2+c^2)}\leq \frac{c^2}{a(b^2+c^2)}+\frac{a^2}{c(a^2+b^2)}\)
Cộng theo vế các BĐT trên:
\(\Rightarrow \text{VT}\leq \frac{b^2+c^2}{a(b^2+c^2)}+\frac{a^2+c^2}{b(a^2+c^2)}+\frac{b^2+a^2}{c(b^2+a^2)}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Ta có đpcm
Dấu "=" xảy ra khi $a=b=c$

