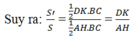Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E M N F 1 2 1 2 3 1
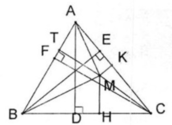
Gọi E là trung điểm của MN. F là giao điểm của ND với AB.
Ta có: DF là phân giác ^ADB, DM là phân giác ^BDC. Mà ^ADB và ^BDC kề bù
=> DF vuông góc với DM => DM vuông góc với DN => Tam giác MDN vuông tại D
DE là trung tuyến của tam giác MDN => DE=ME=NE
=> Tam giác DEM cân tại E => ^EDM=^EMD (1)
^EMD là góc ngoài của tam giác BDM => ^EMD=^D1+^B2. Mà ^D1=^D2 => ^EMD=^D2+^B2 (2)
^EDM=^D2+^D3 (3)
Từ (1); (2) và (3) => ^D2+^B2=^D2+^D3 => ^B2=^D3.
Tam giác ABC cân tại A => ^ABC=^ACB => 1/2^ABC=1/2^ACB => ^B1=^B2=1/2^ACB
=> ^B1=^D3=1/2^ACB (Vì ^B2=^D3)
^DCB là góc ngoài của tam giác CDE => ^DCB=^D3+^E1. Mà ^D3=1/2^ACB=1/2^DCB
=> ^DCB=1/2^DCB+^E1 => ^E1=1/2^DCB hay ^E1=1/2^ACB
Ta thấy: ^B2=1/2^ACB; ^E1=1/2^ACB => ^B2=^E1 => Tam giác BDE cân tại D => BD=DE.
Lại có: DE=1/2MN => BD=1/2MN (đpcm)
~~~~~~~~~~~~ Ai ngang qua nhớ để lại ~~~~~~~~~~
tui cũng hỏi bài này

A B C D H
a) Sử dụng định lí Pita go tính đc BC=10 cm
Vì AD là phân giác góc A , D thuộc Bc nên ta có:
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{8}{6}=\frac{4}{3}\Rightarrow\hept{\begin{cases}BD=\frac{4}{7}.BC=\frac{40}{7}\\CD=\frac{3}{7}.BC=\frac{30}{7}\end{cases}}\) (cm)
b) Xét tam giác AHB và tam giác CHA
có: \(\widehat{AHB}=\widehat{CHA}=90^o\)
\(\widehat{ABH}=\widehat{CAH}\)( cùng phụ góc ACB)
=> tam giác ABH đồng dạng tam giác CHA
c) \(S_{\Delta ABC}=\frac{1}{2}.AH.BC=\frac{1}{2}AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{8.6}{10}=\frac{24}{5}\)(cm)
Xét tam giác AHB vuông và tam giác AHC vuông
Sử dụng định lí pitago để tính \(BH=\frac{32}{5};CH=\frac{18}{5}\)(cm)
\(S_{\Delta AHB}=\frac{1}{2}.AH.BH=\frac{1}{2}.\frac{24}{5}.\frac{32}{5}=\frac{384}{25}\left(cm^2\right)\)
\(S_{\Delta AHC}=\frac{1}{2}.AH.CH=\frac{1}{2}.\frac{24}{5}.\frac{18}{5}=\frac{216}{25}\left(cm^2\right)\)

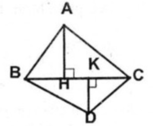
Hai △ ABC và △ DBC có chung canh đáy BC nên ta có:
S A B C = 1/2 AH. BC = S
S D B C = 1/2 DK. BC = S'