Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

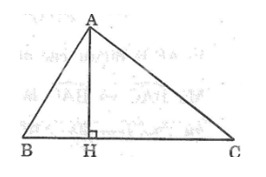
Trong ΔABC ta có ∠AC > ∠AB (gt)
Suy ra: ∠B > ∠C (đối diện cạnh lớn hơn là góc lớn hơn)
Trong ΔAHB có ∠(AHB) = 90o
Suy ra: ∠B + ∠(HAB) = 90o (tính chất tam giác vuông) (1)
Trong ΔAHC có ∠(AHC) = 90o
Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)
Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC) .

(Giải thích ở phần (**): nếu tổng của hai cặp số cùng bằng nhau (bằng 9090o chẳng hạn) thì số nào cộng với số lớn hơn thì nhỏ hơn số kia. Tức là:
a + b = 90o
c + d = 90o
mà b > d thì suy ra a < c)

A B C D H E F
Gộp a) + b) lại cho dễ làm:
Xét hai tam giác ABE và tam giác ACF:
Ta thấy rằng: \(\widehat{BEA}=\widehat{CFA}\)
Mà: \(\widehat{BEA}+\widehat{BAC}+\widehat{ABE}=180^o\Rightarrow\widehat{ABE}=180^o-\widehat{BEA}-\widehat{BAC}\) (tổng ba góc trong tam giác)
\(\widehat{CFA}+\widehat{BAC}+\widehat{ACF}=180^o\Rightarrow\widehat{ACF}=180^o-\widehat{CFA}-\widehat{BAC}=180^o-\widehat{BEA}-\widehat{BAC}=\widehat{ABE}\)
Từ đây,ta có: \(\widehat{ACF}=\widehat{ABE}\).Từ đây kết hợp giả thiết góc ABC > góc ACB suy ra: \(\widehat{ABC}-\widehat{ABE}>\widehat{ACB}-\widehat{ACF}\)
Hay góc EBC > góc FCB . Đầu tiên,ta dễ c/m B,H,E thẳng hàng ,do BE là đường cao xuất phát từ đỉnh B.Lại thấy rằng H là giao điểm của 2 đường cao nên đường cao còn lại cũng đi qua nó.Do vậy H là trực tâm)Ta sẽ c/m C,H, F thẳng hàng để suy ra EBC = HBC > FCB = HCB tức là góc HBC > góc HCB.Để từ đó theo quan hệ giữa góc và cạnh đối diện trong tam giác BHC ta suy ra HC > HB
(mai mình hướng dẫn tiếp,buồn ngủ quá!)
Chứng minh tiếp từ chỗ c/m C, H, F thẳng hàng nhé: (không chắc lắm đâu,mình dốt hình)
Ta có: H là giao điểm của hai đường cao nên đường cao còn lại cũng đi qua H hay H là trực tâm.
Lại có: CH là đoạn thẳng xuất phát từ C đến trực tâm H nên thuộc đường cao xuất phát từ C. (1)
HF là đoạn thẳng hạ từ trực tâm H vuông góc với AB nên thuộc đường cao xuất phát từ C (2)
Từ (1) và (2) suy ra C, H, F thẳng hàng (3)
Từ đây suy ra \(\widehat{EBC}=\widehat{HBC}>\widehat{FCB}=\widehat{HCB}\)
Hay \(\widehat{HBC}>\widehat{HCB}\) vậy theo quan hệ giữa góc và cạnh đối diện trong tam giác BHC ta suy ra HC > HB
b) Theo kết quả của (3) (ở câu a) ta có C, H, F thẳng hàng.
c)Theo giả thiết ở câu a) ta có: \(\widehat{ABC}>\widehat{ACB}\).Theo quan hệ giữa góc và cạnh đối diện của tam giác ABC suy ra AC > AB
Suy ra AC + AB > AB + AB = 2AB (4).
Lại có: Tam giác ABD vuông tại D (giả thiết AD là đường cao hạ từ A vuông góc với BC). Do đó AB là cạnh lớn nhất.
Suy ra AB > AD suy ra 2AB > 2AD (5)
Từ (4) và (5) kết hợp lại,ta có: AC + AB > 2AB > 2AD tức là AC + AB > 2AD.
d) Đang suy nghĩ...

a. Ta có: \(\widehat{HAB}+\widehat{HAD}=\widehat{BAD}\)
\(\widehat{HAC}-\widehat{HAD}=\widehat{DAC}\)
Vì AD là tia phân giác của góc BAC => \(\widehat{BAD}=\widehat{DAC}\) =.> ĐPCM
b. Xét tam giác HAC có \(\widehat{AHC}+\widehat{HCA}+\widehat{HAC}=180\text{đ}\text{ộ}\)
=>\(\widehat{HAC}=180^o-\widehat{AHC}-\widehat{HCA}\)
Xét tam giác HAB có \(\widehat{HAB}+\widehat{ABH}+\widehat{BHA}=180^o\)
=> \(\widehat{HAB}=180^o-\widehat{ABH}-\widehat{BHA}\)
Ta có: \(\widehat{HAC}-\widehat{HAB}=180^o-\widehat{AHC}-\widehat{HAC}-\left(180^o-\widehat{ABH}-\widehat{BHA}\right)\)
\(=180^o-90^o-\widehat{HCA}-180^o+\widehat{ABH}+90^o\)
\(=180^o-180^o+90^o-90^o+\widehat{ABH}-\widehat{HCA}\)
\(=\widehat{ABH}-\widehat{HCA}=>\text{Đ}PCM\)
c. Ta có: \(\dfrac{1}{2}\left(\widehat{ABC}-\widehat{ACB}\right)=\dfrac{\widehat{ABC}-\widehat{ACB}}{2}=\dfrac{\widehat{HAC}-\widehat{HAB}}{2}\)
\(=\dfrac{2\widehat{DAH}}{2}=\widehat{DAH}=>\text{Đ}pcm\)
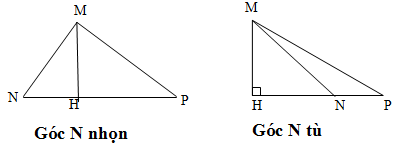

Ta có: AB < AC (gt)
Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)
* Trường hợp góc B nhọn
Trong Δ ABC, ta có: AB < AC
Suy ra: góc B > góc C(đối diện với cạnh lớn hơn là góc lớn hơn)
Trong Δ AHB, ta có góc AHB = \(90^0\)
Suy ra: góc B + góc HAB = \(90^0\) (tính chất tam giác vuông) (1)
Trong Δ AHC, ta có góc AHC = \(90^0\)
Suy ra: góc C + góc HAC = \(90^0\) (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: góc B + góc HAB) = góc C + góc HAC
Mà góc B > góc C nên góc HAB < góc HAC
* Trường hợp Btù
Vì điểm B nằm giữa H và C nên góc HAC = góc HAB + góc BAC
Vậy góc HAB < góc HAC.