Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

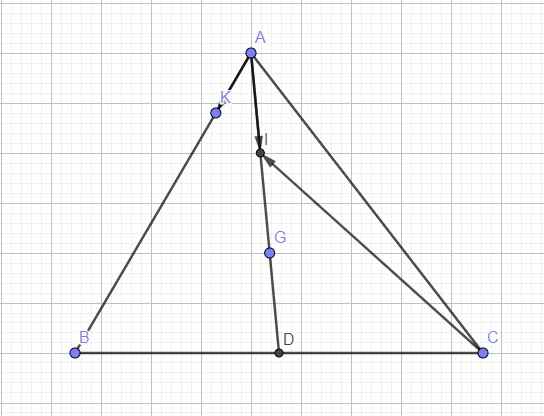
Do G là trọng tâm tam giác
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AD}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{1}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}+\dfrac{1}{3}\overrightarrow{AC}\)
\(=\dfrac{2}{3}\overrightarrow{AC}+\dfrac{1}{3}\overrightarrow{CB}=-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\)
Do I là trung điểm AG
\(\Rightarrow\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AG}=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{3}\overrightarrow{CB}\right)=-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{AK}=\dfrac{1}{5}\overrightarrow{AB}=\dfrac{1}{5}\left(\overrightarrow{AC}+\overrightarrow{CB}\right)=-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)
\(\overrightarrow{CI}=\overrightarrow{CA}+\overrightarrow{AI}=\overrightarrow{CA}-\dfrac{1}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}=\dfrac{2}{3}\overrightarrow{CA}+\dfrac{1}{6}\overrightarrow{CB}\)
\(\overrightarrow{CK}=\overrightarrow{CA}+\overrightarrow{AK}=\overrightarrow{CA}-\dfrac{1}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}=\dfrac{4}{5}\overrightarrow{CA}+\dfrac{1}{5}\overrightarrow{CB}\)

anh tuấn
Vì $M,N, P$ là trung điểm của các cạnh $AB, BC, CA$ nên các cạnh $AB=2NP; BC=2PM; CA=2MN$ theo tính chất đường trung bình.
Khi đó ta nói $\triangle ABC\sim \triangle NPM$ theo tỷ lệ $k=2$ đó bạn.

Cần tính AM theo gì bạn? Vì ở đây có quá nhiều cách biểu diễn AM theo 2 trong 3 cạnh tam giác

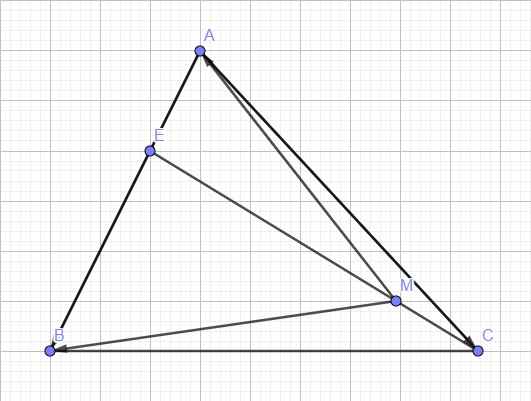
\(\overrightarrow{ME}+3\overrightarrow{MC}=\overrightarrow{0}\Rightarrow\overrightarrow{MC}=-\dfrac{1}{3}\overrightarrow{ME}\)
\(EB=2EA\Rightarrow\overrightarrow{BE}=2\overrightarrow{EA}\)
Ta có: \(\overrightarrow{ME}=\overrightarrow{MB}+\overrightarrow{BE}=\overrightarrow{MB}+2\overrightarrow{EA}=\overrightarrow{MB}+2\left(\overrightarrow{EM}+\overrightarrow{MA}\right)=\overrightarrow{MB}-2\overrightarrow{ME}+2\overrightarrow{MA}\)
\(\Rightarrow3\overrightarrow{ME}=\overrightarrow{MB}+2\overrightarrow{MA}\Rightarrow\overrightarrow{ME}=\dfrac{1}{3}\overrightarrow{MB}+\dfrac{2}{3}\overrightarrow{MA}\)
\(\Rightarrow\overrightarrow{MC}=-\dfrac{1}{3}\overrightarrow{ME}=-\dfrac{1}{9}\overrightarrow{MB}-\dfrac{2}{9}\overrightarrow{MA}\)
\(\Rightarrow\dfrac{2}{9}\overrightarrow{MA}=-\dfrac{1}{9}\overrightarrow{MB}-\overrightarrow{MC}\Rightarrow\overrightarrow{MA}=-\dfrac{1}{2}\overrightarrow{MB}-\dfrac{9}{2}\overrightarrow{MC}\)

A B C G I J
a) \(\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{BA}+3\overrightarrow{IB}=\overrightarrow{0}\Rightarrow\overrightarrow{BI}=\frac{1}{3}\overrightarrow{BA}\)
\(\overrightarrow{CI}=\overrightarrow{CB}+\overrightarrow{BI}=\overrightarrow{CB}+\frac{1}{3}\overrightarrow{BA}=\overrightarrow{CB}+\frac{1}{3}\left(\overrightarrow{CA}-\overrightarrow{CB}\right)=\frac{2}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}\)
\(\overrightarrow{JB}=x\overrightarrow{JC}\Rightarrow\overrightarrow{CB}-\overrightarrow{CJ}=x\overrightarrow{JC}\Rightarrow\overrightarrow{CB}=\left(x-1\right)\overrightarrow{JC}\Rightarrow\overrightarrow{CJ}=\frac{1}{1-x}\overrightarrow{CB}\)
b) \(\overrightarrow{IJ}=\overrightarrow{CJ}-\overrightarrow{CI}=\frac{1}{1-x}\overrightarrow{CB}-\left(\frac{2}{3}\overrightarrow{CB}+\frac{1}{3}\overrightarrow{CA}\right)=\frac{2x+1}{3\left(1-x\right)}\overrightarrow{CB}-\frac{1}{3}\overrightarrow{CA}\)
c) Dễ có \(\overrightarrow{CG}=\frac{2}{3}\left(\overrightarrow{CB}+\overrightarrow{CA}\right)\). Để \(\overrightarrow{IJ}\)//\(\overrightarrow{CG}\) thì :
\(\frac{\frac{2}{3}}{\frac{2x+1}{3\left(1-x\right)}}=\frac{\frac{2}{3}}{-\frac{1}{3}}\Leftrightarrow\frac{1-x}{2x+1}=-1\Rightarrow2x+1=x-1\Leftrightarrow x=-2\)
Vậy \(x=-2\)tức \(\overrightarrow{JB}=-2\overrightarrow{JC}\)thì IJ // CG.
* Nhận xét: Nếu \(\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b};\overrightarrow{v}=m\overrightarrow{a}+n\overrightarrow{b}\)thì \(\overrightarrow{u}\)//\(\overrightarrow{v}\)\(\Leftrightarrow\frac{x}{m}=\frac{y}{n}.\)