Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét đường tròn (O) có: OM là trung tuyến ứng với AC; AC là dây ko đi qua tâm
\(\Rightarrow\) OM \(\perp\) AC (quan hệ vuông góc giữa đk và dây) (1)
Xét đường tròn (O) có: \(\Delta\)ACD nội tiếp; AD là đường kính
\(\Rightarrow\) \(\Delta\)ACD vuông tại C (sự xđ đường tròn)
\(\Rightarrow\) DC \(\perp\) AC (2)
Từ (1); (2) \(\Rightarrow\) OM//DC (quan hệ từ vuông góc đến //)
Chúc bn học tốt!
1) Vì AD là đường kính của (O) nên O là trung điểm của AD
Xét ΔADC có
O là trung điểm của AD(cmt)
M là trung điểm của AC(gt)
Do đó: OM là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)
hay OM//DC(Định lí 2 về đường trung bình của tam giác)


Đường tròn c: Đường tròn qua A, B, C Đoạn thẳng f: Đoạn thẳng [A, B] Đoạn thẳng g: Đoạn thẳng [B, C] Đoạn thẳng h: Đoạn thẳng [A, C] Đoạn thẳng k: Đoạn thẳng [A, I] Đoạn thẳng l: Đoạn thẳng [B, K] Đoạn thẳng m: Đoạn thẳng [H, C] Đoạn thẳng n: Đoạn thẳng [K, C] Đoạn thẳng p: Đoạn thẳng [I, C] Đoạn thẳng q: Đoạn thẳng [K, I] Đoạn thẳng r: Đoạn thẳng [A, K] Đoạn thẳng t: Đoạn thẳng [B, F] Đoạn thẳng a: Đoạn thẳng [H, F] A = (-6.94, 5.84) A = (-6.94, 5.84) A = (-6.94, 5.84) B = (-8.06, 1.8) B = (-8.06, 1.8) B = (-8.06, 1.8) C = (-1.34, 1.82) C = (-1.34, 1.82) C = (-1.34, 1.82) Điểm D: Giao điểm của i, g Điểm D: Giao điểm của i, g Điểm D: Giao điểm của i, g Điểm E: Giao điểm của j, h Điểm E: Giao điểm của j, h Điểm E: Giao điểm của j, h Điểm H: Giao điểm của i, j Điểm H: Giao điểm của i, j Điểm H: Giao điểm của i, j Điểm K: Giao điểm của c, j Điểm K: Giao điểm của c, j Điểm K: Giao điểm của c, j Điểm I: Giao điểm của c, i Điểm I: Giao điểm của c, i Điểm I: Giao điểm của c, i Điểm J: Trung điểm của m Điểm J: Trung điểm của m Điểm J: Trung điểm của m Điểm O: Tâm của c Điểm O: Tâm của c Điểm O: Tâm của c Điểm F: Giao điểm của c, s Điểm F: Giao điểm của c, s Điểm F: Giao điểm của c, s Điểm P: Trung điểm của A, C Điểm P: Trung điểm của A, C Điểm P: Trung điểm của A, C
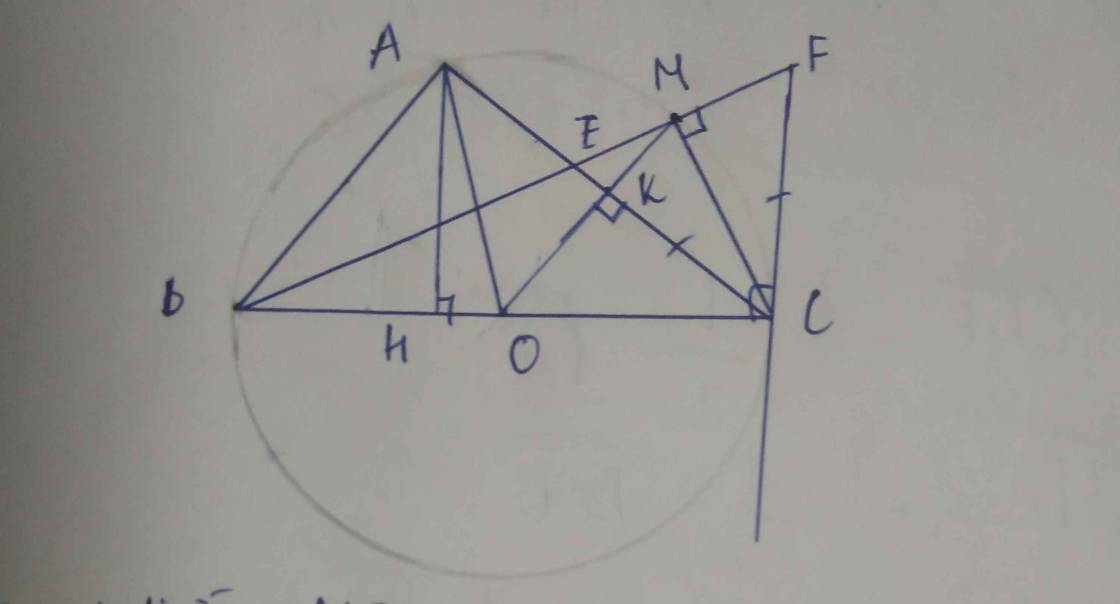
a. Ta thấy \(\widehat{HDC}=\widehat{HEC}=90^o\) nên CDHE là tứ giác nội tiếp đường tròn đường kính HC.
b. Ta thấy ngay \(\widehat{IAC}=\widehat{KBC}\) (Cùng phụ với góc ACB) nên \(\widebat{IC}=\widebat{KC}\) (Góc nội tiếp)
suy ra IC = KC ( Liên hệ giữa cung và dây)
Vậy nên tam giác IKC cân tại C.
c. Do \(\widebat{IC}=\widebat{KC}\) nên \(\widehat{KAC}=\widehat{ACI}\) (Góc nội tiếp)
Xét tam giác AHK có AE vừa là đường cao, vừa là phân giác nên AHK là tam giác cân tại A, hay AH = AK.
d. Ta thấy do BOF là đường kính nên \(\widehat{BCF}=90^o\Rightarrow\) AH // FC (Cùng vuông góc với BC).
Tương tự AF // HC vì cùng vuông góc với AB. Vậy thì AFCH là hình bình hành hay AC giao FH tại trung điểm mỗi đường.
P là trung điểm AC nên F cũng là trung điểm FH. Vậy F, H, P thẳng hàng.