Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình vẽ : tự vẽ nha
Sabc = \(\frac{1}{2}AH.BC=\frac{1}{2}BK.AC\)
=> \(AH.BC=AC.BK\)
=> \(\frac{AH}{BK}=\frac{AC}{BC}=\frac{15.6}{12}=\frac{13}{10}\)
=> \(\frac{AC}{13}=\frac{BC}{10}=t\)
=> \(AC=13t;BC=10t\)
Tam giác ABC cân có AH là đg cao => AH là t tuyến => BH = HC = 1/2 BC = 1/2.10t = 5t
TAm giác AHC vuông tại H , theo py ta go :
\(AC^2-HC^2=15.6^2\)
=> \(169t^2-25t^2=15.6^2\)
tính ra t thay vào tìm ra BC
2SABC = AH.BC = AC.BK
ð 15,6BC = 12AC
ð BC = 12/15,6AC
ð CH = 6/15,6AC
ð AH2 = AC2 – HC2 = 144/169AC2
ð AH = 12/13 AC
ð 15,6 = 12/13AC
ð AC = 16,9
ð BC = 12/15,6 AC = 13

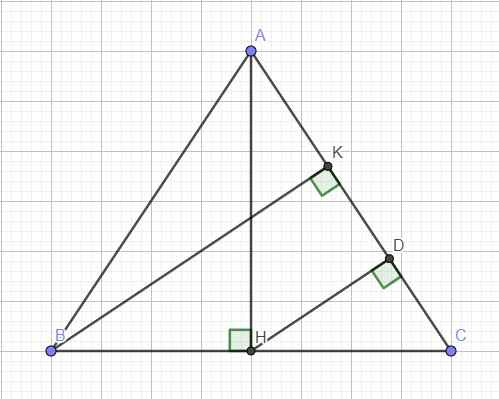
Do tam giác ABC cân tại A nên AH là đường cao đồng thời là trung tuyến
Hay H là trung điểm BC \(\Rightarrow CH=\dfrac{BC}{2}\)
Từ H hạ HD vuông góc AC
\(\Rightarrow HD||BK\) (cùng vuông góc AC)
\(\Rightarrow\) HD là đường trung bình tam giác ACH
\(\Rightarrow HD=\dfrac{BK}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông ACH:
\(\dfrac{1}{HD^2}=\dfrac{1}{AH^2}+\dfrac{1}{CH^2}\)
\(\Rightarrow\dfrac{1}{\left(\dfrac{BK}{2}\right)^2}=\dfrac{1}{AH^2}+\dfrac{1}{\left(\dfrac{BC}{2}\right)^2}\Rightarrow\dfrac{4}{BK^2}=\dfrac{1}{AH^2}+\dfrac{4}{BC^2}\)
\(\Rightarrow\dfrac{1}{BK^2}=\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}\)