Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(AB^2=BH.BC=BH\left(BH+HC\right)\)\(\Leftrightarrow20^2=BH^2+9BH\Leftrightarrow BH^2+9BH-400=0\)
\(\Leftrightarrow BH=16cm\)
\(\Rightarrow BC=HC+HB=9+16=25cm\)
\(\Rightarrow AH^2=HB.HC\Leftrightarrow AH=\sqrt{HB.HC}=12cm\)


Áp dụng hệ thực giữa cạnh và đường cao trong tam giác vuông có:
\(AH^2=AB.BH\)
\(\Leftrightarrow20^2=BH\left(BH+9\right)\)
\(\Leftrightarrow BH^2+94H-400=0\)
\(\Rightarrow BH=16\left(cm\right)\)
Lại có: \(BC=BH+HC=16+9=25\left(cm\right)\)
\(\Rightarrow AH^2=BH.CH=16.9=12^2\)
\(\Rightarrow AH=12\left(cm\right)\)

Gọi AC=a;BH=b
thì ta có hệ pt \(\sqrt{a^2+20^2}=9+b\)(pytago)
\(\frac{20a}{b+9}=\sqrt{9b}\)(hệ thức lượng trong tam giác vuông)

v~
ta có \(AB^2=BH.BC=BH.\left(BH+9\right)=BH^2+9BH\)
\(BH^2+9BH-AB^2=0\)
\(\Leftrightarrow BH^2+9BH-20^2=0\Leftrightarrow BH^2+9BH-400=0\)
\(\Leftrightarrow BH^2-16BH+25BH-400=0\)
\(\Leftrightarrow BH\left(BH-16\right)+25\left(BH-16\right)=0\)
\(\Leftrightarrow\left(BH-16\right)\left(BH+25\right)=0\)
=> BH = 16 VÀ BH = -25 ( loại )
=> BH = 16
\(AH=\sqrt{AB^2-BH^2}=\sqrt{20^2-16^2}=12\)
CHỖ NÀO KO HỈU HỎI LẠI MIK NHAN !!!

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\cdot\left(BH+9\right)=20^2\)
\(\Leftrightarrow BH^2+9BH-400=0\)
\(\Leftrightarrow BH^2+25BH-16BH-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AH^2=20^2-16^2=144\)
hay AH=12(cm)

Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:AB^2+AB^2=BC^2 Hay: 12^2+5^2=169=BC^2 => BC=13cm ÁP dụng hệ thức ta có: +) AB^2=BH.BC Hay: BH=AB^2:BC=144:13 =144/13(cm) Ta có CH=BC-BH=13-144/13=25/13(cm)

C A B H 2 8
Áp dụng hệ thức liên quan tới đường cao ta có :
\(AH^2=BH.CH=2.8=16\)
\(\Rightarrow AH=4cm\)
Áp dụng công thức \(AH^2=BH.CH\) (hệ thức về cạnh trong tam giác vuông)
Được : \(AH^2=8.2=16\Rightarrow AH=4\) (cm)
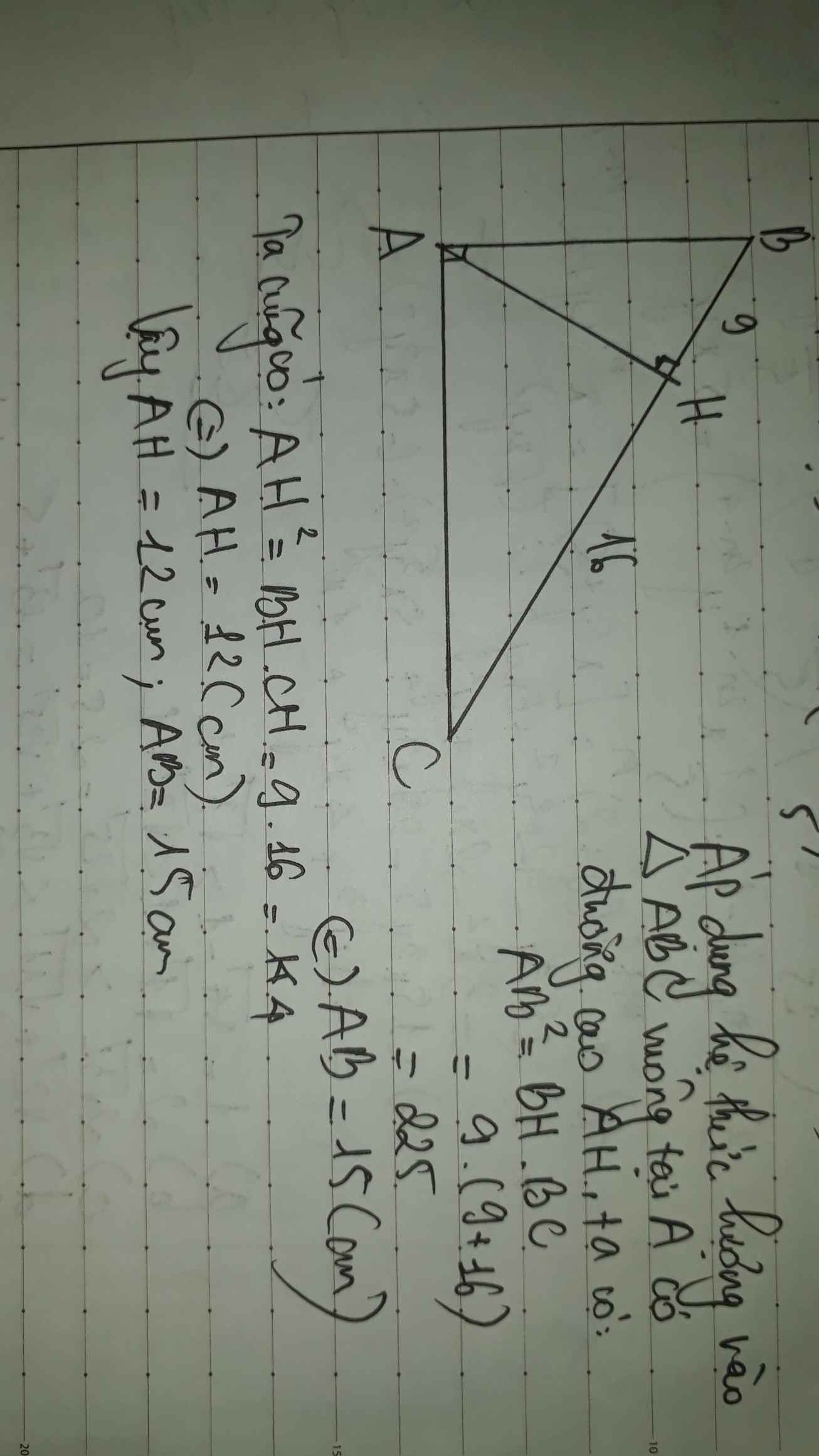

Áp dụng hệ thực giữa cạnh và đường cao trong tam giác vuông có:
\(AH^2=AB.BH\)
\(\Leftrightarrow20^2=BH\left(BH+9\right)\)
\(\Leftrightarrow BH^2+94H-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
Lại có: \(BC=BH+HC=16+9=25\left(cm\right)\)
\(\Rightarrow AH^2=BH.CH=16.9=12^2\)
\(\Rightarrow AH=12\left(cm\right)\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB^2=BH.BC
<=>20^2=BH.(BH + 9)
<=>BH^2 + 9BH-400=0
=> BH=16cm
Mà BC=BH + HC=16 + 9=25cm
AH^2 = BH.HC = 16.9 = 12^2
suy ra AH = 12cm.
Vậy AH=12cm.