Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì \(\Delta=(m-2)^2+12>0, \forall m\in\mathbb{R}\) nên pt luôn có 2 nghiệm phân biệt $x_1,x_2$ với mọi $m$
Áp dụng định lý Vi-et: \(\left\{\begin{matrix} x_1+x_2=m-2\\ x_1x_2=-3\end{matrix}\right.\)
Khi đó:
\(\sqrt{x_1^2+2018}-x_1=\sqrt{x_2^2+2018}+x_2\)
\(\Leftrightarrow (\sqrt{x_1^2+2018}-\sqrt{x_2^2+2018})-(x_1+x_2)=0\)
\(\Leftrightarrow \frac{x_1^2-x_2^2}{\sqrt{x_1^2+2018}+\sqrt{x_2^2+2018}}-(x_1+x_2)=0\)
\(\Leftrightarrow (x_1+x_2)\left(\frac{x_1-x_2}{\sqrt{x_1^2+2018}+\sqrt{x_2^2+2018}}-1\right)=0\)
\(\Leftrightarrow \left[\begin{matrix} x_1+x_2=m-2=0(1)\\ x_1-x_2=\sqrt{x_1^2+2018}+\sqrt{x_2^2+2018}(2)\end{matrix}\right.\)
\((1)\Leftrightarrow m=2\) (t/m)
\((2)\Leftrightarrow \sqrt{x_1^2+2018}-x_1=-(\sqrt{x_2^2+2018}+x_2)=-(\sqrt{x_1^2+2018}-x_1)\)
\(\Leftrightarrow \sqrt{x_1^2+2018}=x_1\) (vô lý)
Vậy $m=2$

\(\Delta=\left(2-m\right)^2-4.\left(-3\right)=\left(m-2\right)^2+12\ge0\) luôn đúng
Do đó pt luôn có hai nghiệm \(x_1,x_2\) với mọi m
Ta có : \(\sqrt{x_1^2+2018}-x_1=\sqrt{x_2^2+2018}+x_2\)
\(\Leftrightarrow\)\(x_1^2+2018-2\sqrt{\left(x_1^2+2018\right)\left(x_2^2+2018\right)}+x_2^2+2018=x_1^2+2x_1x_2+x_2^2\)
\(\Leftrightarrow\)\(2018-\sqrt{\left(x_1x_2\right)^2+2018\left(x_1+x_2\right)^2-4036x_1x_2+2018^2}=x_1x_2\) (*)
Theo định lý Vi-et ta có : \(\hept{\begin{cases}x_1+x_2=m-2\\x_1x_2=-3\end{cases}}\)
(*) \(\Leftrightarrow\)\(2018-\sqrt{\left(-3\right)^2+2018\left(m-2\right)^2-4036.\left(-3\right)+2018^2}=-3\)
\(\Leftrightarrow\)\(9+2018\left(m-2\right)^2+12108+2018^2=2021^2\)
\(\Leftrightarrow\)\(2018\left(m-2\right)^2=0\)
\(\Leftrightarrow\)\(m=2\)
Vậy với m=2 thì hai nghiệm pt thoả mãn \(\sqrt{x_1^2+2018}-x_1=\sqrt{x_2^2+2018}+x_2\)

Thấy \(\Delta=b^2-4ac=\left(m-2\right)^2-4\left(-3\right)=m^2-4m+16>0\left(\forall m\in R\right)\)
Có: Hệ thức\(\Leftrightarrow\)\(\left(x_1+x_2\right)\left(1-\dfrac{x_1-x_2}{\sqrt{x_1^2+2018}+\sqrt{x_2^2+2018}}\right)=0\\ \Rightarrow x_1+x_2=0\left(1-\dfrac{x_1-x_2}{\sqrt{x_1^2+2018}+\sqrt{x_2^2+2018}}\ne0\right)\)
Áp dụng hệ thức Vi-ét:
\(0=x_1+x_2=-\dfrac{b}{a}=m-2\\ \Rightarrow m=2\)

\(\Delta=m^2+12>0\) ; \(\forall m\)
\(\Rightarrow\) Khi \(n=0\) thì pt có nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=n-3\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1-x_2=1\\x_1^2-x_2^2=7\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1-x_2=1\\\left(x_1+x_2\right)\left(x_1-x_2\right)=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1-x_2=1\\x_1+x_2=7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=3\end{matrix}\right.\)
Thế vào hệ thức Viet: \(\left\{{}\begin{matrix}4+3=-m\\4.3=n-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m=-7\\n=15\end{matrix}\right.\)
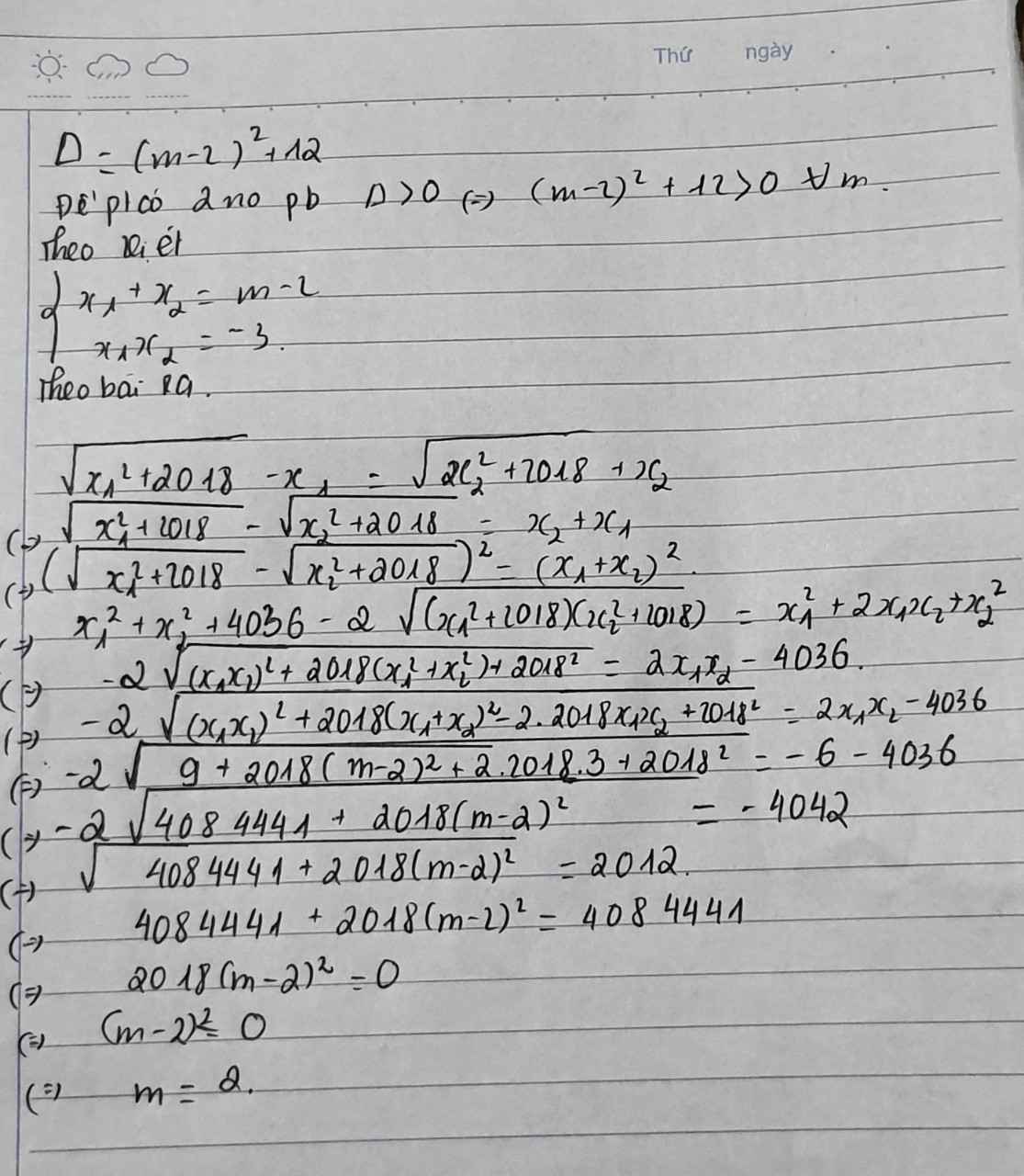
\(\Delta=\left(n-2\right)^2+12>0\) ; \(\forall n\Rightarrow\) pt đã cho luôn có 2 nghiệm pb trái dấu với mọi n
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=n-2\\x_1x_2=-3\end{matrix}\right.\)
\(\sqrt{x_1^2+2018}-x_2=\sqrt{x_2^2+2018}+x_1\)
\(\Rightarrow x_1^2+x_2^2-2x_2\sqrt{x_1^2+2018}=x_1^2+x_2^2+2018+2x_1\sqrt{x_2^2+2018}\)
\(\Rightarrow-x_2\sqrt{x_1^2+2018}=x_1\sqrt{x_2^2+2018}\)
\(\Rightarrow x_2^2\left(x_1^2+2018\right)=x_1^2\left(x_2^2+2018\right)\)
\(\Rightarrow x_1^2=x_2^2\Rightarrow x_1=-x_2\) (do \(x_1;x_2\) trái dấu)
\(\Rightarrow x_1+x_2=0\Rightarrow n-2=0\Rightarrow n=2\)
Thử lại với \(n=2\) thấy đúng. Vậy...
mình không hiểu lắm ngay từ bước đầu, có thể giãi rõ hơn nữa không?