Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
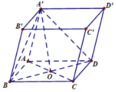
Do A B ' ∩ A ' B cắt nhau tại trung điểm mỗi đường.
Do đó d B ' = d A = d C
+) Dựng C H ⊥ B D ⇒ C H ⊥ ( A ' B D )
+) Do đó
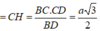
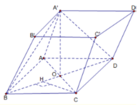
Gọi O là giao điểm của AC và BD \(\Rightarrow A_1O\perp\left(ABCD\right)\)
Gọi E là trung điểm của AD \(\Rightarrow\begin{cases}OE\perp AD\\A_1E\perp AD\end{cases}\)
Suy ra \(\widehat{A_1EO}\) là góc giữa 2 mặt phẳng \(\left(ADD_1A_1\right)\) và \(\left(ABCD\right)\) \(\Rightarrow\widehat{A_1EO}=60^o\)
Suy ra : \(A_1O=OE.\tan\widehat{A_1EO}=\frac{AB}{2}\tan\widehat{A_1EO}=\frac{a\sqrt{3}}{2}\)
Diện tích đáy \(S_{ABCD}=AB.AD=a^2\sqrt{3}\)
Thể tích \(V_{ABCD.A'B'C'D'}=S_{ABCD}.A_1O=\frac{3a^2}{2}\)
Ta có : \(B_1C||A_1D\)\(\Rightarrow B_1C||\left(A_1CD\right)\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=d\left(C,\left(A_1BD\right)\right)=CH\)
\(\Rightarrow d\left(B_1,\right)\left(A_1BD\right)=CH=\frac{CD.CB}{\sqrt{CD^2+CB^2}}=\frac{a\sqrt{3}}{2}\)
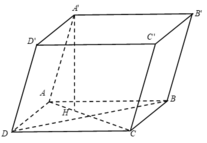
Đáp án A
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a.
Ta có:
=> A'A = a 3 . 3 = 3a => V = 3π a 3
Đáp án là A
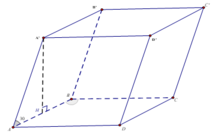
+ Tính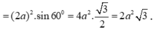 
+ Tính A'H:
Ta có: 
( Vì AH là hình chiếu của AA' trên mp(ABCD)).
Suy ra: 
Vậy: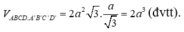 
Đáp án là C
Gọi H là hình chiếu của A’ trên (ABCD). Dễ thấy góc
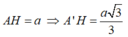
Dễ dàng tính được diện tích đáy
Đáp án D
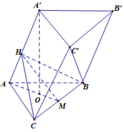
Gọi M là trung điểm BC.
Từ M kẻ M H ⊥ A A ' ⇒ ( H B C ) ⊥ A A '
Vậy thể tích A B C A ' B ' C ' là
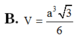
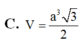
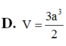
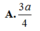
m.n giúp e với ạ