NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
13 tháng 12 2018
Áp dụng định lí Py-ta-go trong ΔACD vuông tại D ta có:
AC2 = AD2 + CD2 = 482 + 362 = 2304 + 1296 = 3600
⇒ AC = 60(cm)
25 tháng 6 2021
Bài 1 : A B C D 4
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
25 tháng 6 2021
Bài 2 :
A B C D 3 căn27
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm
20 tháng 5 2020
A B C D 48 36
XÉT TAM GIÁC DAC (\(\widehat{D}=90^O\)) CÓ
\(AC^2=AD^2+DC^2\)(ĐỊNH LÍ PY-TA-GO)
\(\Rightarrow AC^2=48^2+36^2\)
\(\Rightarrow AC^2=3600\)
\(\Rightarrow AC=60\)
VẬY ĐỘ DÀI AC LÀ 60cm
DD
4
19 tháng 1 2022
tớ gợi ý nhé:
gọi hai cạnh góc vuông là a;b, cạnh huyền là c
đặt a/2= b/4 vào k
=> a=....; b= .....
sau đó là áp dụng đl pi-ta-go( ghép hết vào với nhau),tính c
Thế là xong
TT
20 tháng 4 2017
độ dài đường chéo AC là
\(\sqrt{48^2+36^2}=\sqrt{2304+1296}=\sqrt{3600}=60\)(cm)
vậy độ dài đường chéo AC là 60cm
20 tháng 4 2017
Giải:
Theo định lí Pytago, ta có:
AC2= AD2 +CD2
= 482 + 362
= 2304 + 1296= 3600
AC= 60 (cm)
P
4
2 tháng 12 2021
Gọi cd,cr lần lượt là a,b(cm;a,b>0)
Áp dụng tc dtsbn:
\(\dfrac{a}{5}=\dfrac{b}{3}=\dfrac{2\left(a+b\right)}{2\left(5+3\right)}=\dfrac{48}{16}=3\\ \Leftrightarrow\left\{{}\begin{matrix}a=15\\b=9\end{matrix}\right.\)
Vậy ...
CM
18 tháng 1 2017
Gọi độ dài chiều rộng và chiều dài của hình chữ nhật là x, y (cm)
Theo đầu bài ta có:
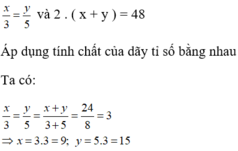
Chọn đáp án A
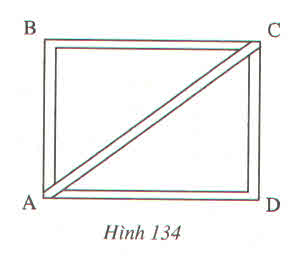
Vì ABCD là hcn => AB = CD = 36 cm
Theo định lí Pytago tam giác ADC vuông tại D
\(AC=\sqrt{AD^2+DC^2}=60cm\)